问题描述

现在有一份数据，$x_i$是数据的特征，y是分类0或1，这是一个二分类问题。我们希望训练一个模型，当有新的数据的时候，判断数据的分类是0，还是1。

x1	x2	y
-0.017612	14.053064	0
-1.395634	4.662541	1
-0.752157	6.538620	0
-1.322371	7.152853	0
0.423363	11.054677	0
0.406704	7.067335	1
0.667394	12.741452	0
-2.460150	6.866805	1
0.569411	9.548755	0
-0.026632	10.427743	0
...	...	...

这里的数据只有两个特征值，我们可以在二维图像上画出来。如下图，如果只有两个特征，而数据是线性可分的就可以用一条直线将数据划分开来。如果不止两个特征呢?如果有更多的特征，比如有ｋ个，那么在ｋ维的空间中线性可分的数据也会有一个超平面可以将数据分割开来。
　　那么这个超平面可以表示为$z = w_1x_1+w_2x_2+w_3x_3+....+w_kx_k + b$,如果用向量表示则可以写成$z=w^T x + b$

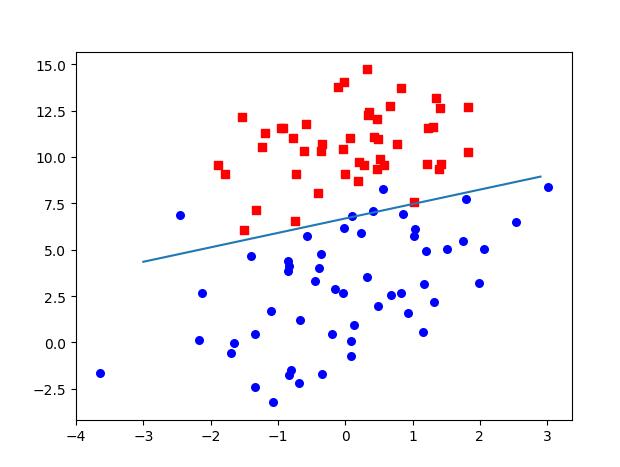数据点

预备知识

sigma函数

我们需要一个函数输出0和1来预测类别，理想状态下单位阶跃函数符合这个需求，
$$f(x) = \left{
\begin{aligned}
0 & = & x < 0 \
0.5 & = & x = 0 \
1 & = & x > 0
\end{aligned}
\right.$$
　　但是后续的计算需要这个函数是一个可微的函数，显然单位阶跃函数不符合这个需求，我们希望能找到一个近似单位阶跃函数并且连续可微的函数，simga函数有很好的性质符合我们的需求。
$$\sigma(z) = \frac{1}{1+e^{-z}}$$
　　当输入z=0时，返回0.5，当z越大，$\sigma$逼近1,当z减小$\sigma$逼近0,

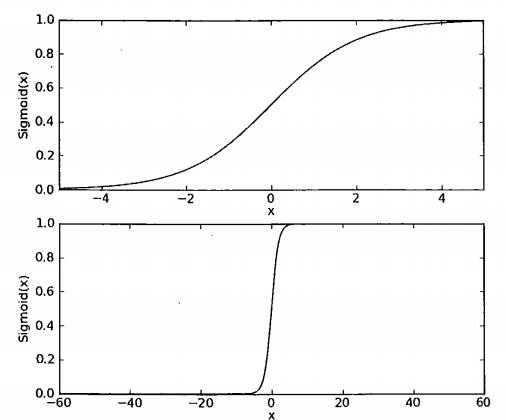两种尺度下的sigma函数，当尺度足够大时，sigma看起来就像阶跃函数

两种尺度下的sigma函数，当尺度足够大时，sigma看起来就像阶跃函数
$\sigma(z) = \frac{1}{1+e^{{-z}}$的输入为z,而$z=w}T x$ ,那么现在问题就变成，怎么找到最优的$w$,这里我们把$w$称为回归系数。
　　将$z=w^T x$带入$\sigma(z)$得到
$$h_w(x) = \frac{1}{1+e^{wT x + b}}$$
　　上式可以转换为　$$ln(\frac{h_w(x)}{1-h_w(x)}) = w^Tx + b$$
　　若将 y 视为样本 x 作为正例的可能性，则 1-h_w(x) 是其反例可能性,两者的比值$\frac{h_w(x)}{1-h_w(x)}$,称为"几率" (odds) ，反映了 m 作为正例的相对可能性.对几率取对数则得到
"对数几率" (log odds，亦称 logit),$ln(\frac{h_w(x)}{1-h_w(x)})$

由此可看出，上式实际上是在用线性回归模型的预测结果去逼近,真实标记的对数几率，因此，其对应的模型称为"对数几率回归" (logistic regression，亦称 logit regression) .特别需注意到，虽然它的名字是"回归"，但实际却是一种分类学习方法.这种方法有很多优点，例如它是直接对分类可能性进行建模，无需事先假设数据分布?这样就避免了假设分布不准确所带来的问题;它不是仅预测出"类别"，而是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用;此外，对率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可直接用于求取最优解.

若将式 (3.18) 中的 y 视为类后验概率估计 $p(y =1|x)$ ，则
$$ln(\frac{p(y=1|x)}{p(y=0|x)}) = w^Tx+b$$
显然
$$p(y=1|x) = h_w(x)$$
$$p(y=0|x) = 1-h_w(x)$$
　　于是可以通过极大似然法来估计w和b,对率回归模型最大化"对数似然" (loglikelihood)
$$l(w) = \sum^m_{i=1}(y_ilogh_w(x_i) +(1-y_i)log(1-h_w(x_i)) )$$
　　好了我们现在的目标就是求得系数ｗ使得$l(w)$最大。

基于最优化方法确定回归系数

梯度下降求最小值

现在我们使用最优化方法中的梯度下降法来寻找最优回归系数。梯度下降法的思想是:要找到某个函数的最小值，最好的方法是沿着该函数的某一点上减少最快的方向,及梯度方向寻找。
1.梯度
　　那么梯度怎么得到呢？增长最快的方向，在单变量的函数(如$f(x)=3x^2+4x+1$这样的函数)上就是导数。但是我们的函数有n个变量，这时需要计算函数的偏导数,用$\bigtriangledown f(x_1,x_2)$表示偏导数。
2.梯度下降
　　一开始可以赋予$w$一个随机值,然后在每次迭代的时候将$w$向变化最快的方向移动就可以。用向量表示的话可以写成$w = w - \alpha \bigtriangledown_w f(w)$,$\alpha$控制了每次变化的大小。变化了流程如下图所示。

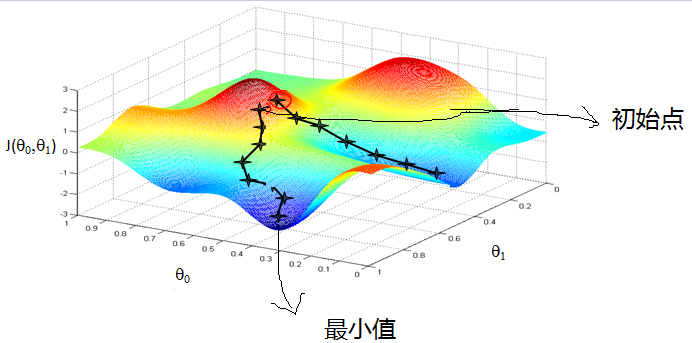enter description here

回头看之前的似然函数
$$l(w) = \sum^m_{i=1}(y_ilogh_w(x_i) +(1-y_i)log(1-h_w(x_i)) )$$
　　现在需要计算w的梯度。
$$ \begin{aligned}
\frac{ \delta (l(w))}{\delta w} &= -\frac{1}{m}\frac{ \delta (\sum^m_{i=1}(y_ilogh_w(x_i) +(1-y_i)log(1-h_w(x_i)) ))}{\delta w} \
&= -\frac{1}{m}\sum^m_{i=1}(y_i \frac{1}{h_w(x_i)} +(1-y_i)\frac{1}{1-h_w(x_i)} )\frac{\delta h_w(x_i) }{\delta w} \
&= -\frac{1}{m}\sum^m_{i=1}(y_i \frac{1}{\sigma(z(x_i))} +(1-y_i)\frac{1}{1-\sigma(z(x_i))} )\frac{\delta \sigma(z(x_i))}{\delta w} \
&= -\frac{1}{m}\sum^m_{i=1}(y_i \frac{1}{\sigma(z(x_i))} +(1-y_i)\frac{1}{1-\sigma(z(x_i))} )(1-\sigma(z(x_i)) \sigma(z(x_i))\frac{\delta z(x_i) }{\delta w} \
&= -\frac{1}{m}\sum^m_{i=1}(y_i (1-\sigma(z(x_i))) +(1-y_i)(\sigma(z(x_i))) )x_i \
&= -\frac{1}{m}\sum^m_{i=1}(y_i - \sigma(z(x_i)) )x_i \
&= \frac{1}{m}\sum^m_{i=1}(h_w(x)-y_i)x_i \
\end{aligned}$$

那么现在w的更新过程可以写成$w = w - \alpha \frac{1}{m} \sum(h_w(x_i)-y_i)x_i$,

实现

1.sigma函数
　　输入X是numpy.array类型数据，可以直接按照向量化来计算

def simgoid(X):
    return 1.0 / (1.0 + exp(-X))

2.梯度上升
这里$w$初始化为1,$w = w - \alpha \frac{1}{m} \sum(h_w(x_i)-y_i)x_i$的计算将数据向量化计算。

def gradAscent(dataSet,labels):
    dataMat = mat(dataSet)
    labelMat = mat(labels).transpose()
    s = shape(dataMat)
    weights = ones((s[1],1))
    maxStep = 500
    alpha = 0.001
    for i in range(maxStep):
        h = simgoid(dataMat*weights)
        error = labelMat - h
        weights = weights + alpha*dataMat.transpose()*error
    return weights

完整代码