许多的语言都有好几种不同的数字类型,比如C++,分别有int,float和double,外加各种变种long int, unsigned等等,实在是繁多,不过,JavaScript中,就只有一种数字类型——number。
比如,我们在浏览器的console中敲下下列代码.
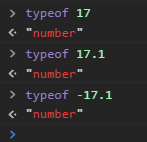
实际上,所有的数字类型,在JavaScript中,都是双倍精度的浮点数类型,就和前面提到的C++的double一样.按照标准,就是每一个数字,都是使用64位(8字节)来存储.
要理解JavaScript中数字存储特性,我们首先需要复习一下,在计算机中,是如何使用二进制来保存浮点数的.
浮点数的二进制表示
现今计算机浮点数的表示,都是采用了IEEE754标准,一个由Intel主导开发的标准,有兴趣的同学可以了解一下上个世纪80年代的各种不同公司对于浮点数的表示,不过现在都已经按照标准来进行处理了.
任意一个浮点数都可以表示成如下的形式.
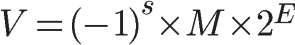
- 符号位(sign) (-1)^s表示的是符号位,当s=0时,V是正数,当s=1时,v为负数.
- 有效位(significand) M表示有效数字,范围是[1,2)或者是[0,1)
-
指数(exponent) 2^E表示指数位.E的作用是对浮点数加权。
这种表示方式非常适合用于处理非常大或者非常接近0的数字.
了解的公式的表示,接下来,我们就可以对浮点数的位按照上述的三个变量进行划分,分别对其进行编码: - 1个单独的符号位s用于编码符号s.
- k位阶码字段,用以编码指数E.
- n位幂字段,用以编码尾数M.
下面,我们用C语言中的单精度浮点数(float)以及双精度浮点数(double)进行说明.
单精度浮点数使用32bit来进行存储,分别s=1, k=8以及n=23.其存储结构如下图所示

32位的存储空间被分割成了三个部分,也就是对应上面所说的s,k以及n.
双精度浮点数则是使用32位进行存储,分别是s=1, k=11, n=52.
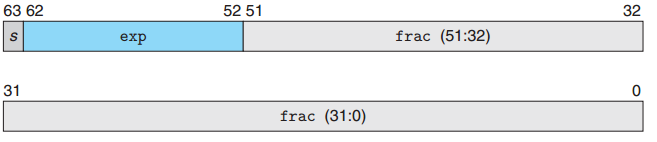
为了简单起见,接下来使用单精度浮点数来进行说明.
单精度浮点数一共表示4种类型的数值,分别是:
-
规范化(Normalized)

-
非规范化(Denormalized)

-
无穷(Infinity)

- 非数字(NaN)

严格来说,Infinity以及NaN属于同一类,因为他们的k相同,都是1,只是n上面的值不一样,一个是全是0,另外一个全是1.
具体上就不展开讲了,以后会另外开一篇新的文章来进行详细讲述计算机底层对于浮点数的存取.现在仍旧是Javascript的主场.我们要知道一点就是,根据浮点数的二进制表示形式,有一部分值是无法完全使用二进制准确表示的.就好比1/3这个值,在十进制上面,我们只能不断的用0.3333333来无限循环表示,但是计算机表示一个浮点数的位是有限的,所以需要对多余的位进行截取,这一点就是误差的来源.
知道了计算机中浮点数的二进制表示,我们都不难理解一些问题了,比如,JavaScript中的数字范围是从-2^53到2^53.因此,JavaScript中的数字是非常适合用以做数学运算的,因为范围非常的大,不容易导致溢出的问题.
位运算操作
许多的数学运算,都是以浮点数的形式直接计算的,比如:
0.1 * 1.9 // 0.19
-99 + 100 // 1
21 - 12.3 //8.7
但是,对于位运算则是比较特别,对于位运算,JavaScript会首先把浮点数转换成32位的整型来进行处理,而不是直接对浮点型进行操作.准确的来说,是转换成32位,大端序, 补码的整型.(这里涉及到比较多操作系统的概念).
举个例子
8 | 1 // 9
这个看起来很简单的操作,8与1进行或运算,实际上经历了好几步的运算,才得到结果9,并不是一下子得出结果的.
正如前面所说,8和1一开始是64位的double,但是,他们在位运算的时候,会被转换成32位的整型,对于数字8,则会转换成00000000000000000000000000001000,我们可以验证一下
(8).toString(2); // "1000"
同理,1则会转换成00000000000000000000000000000001,把这两个数分别按位进行或运算
00000000000000000000000000001000
00000000000000000000000000000001
--------------------------------
00000000000000000000000000001001
就会得到1001这一个数字,我们使用parseInt("1001", 2)对其进行转换,结果就是9.
所有的位运算,都是按照上面所说的这一种方式来进行处理的.
- 把操作数转换成32位整型
- 按位进行位运算
- 把得到的结果转换会JavaScript浮点型属性.
因为这些转换都依赖于JavaScript的引擎,所以有部分引擎经过优化,就会把部分算术运算的操作数用整型来存储,从而避免了一些无谓的转换.
浮点数运算,可靠吗?
说了这么多,什么64位双精度浮点数,计算机储存的方式等等,那么,JavaScript中的浮点数运算,可靠吗?先来看一个例子:
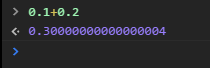
为什么上面得出的结果不是0.3,而是后面跟了一大堆0,后面还有个4?前面我们谈到了浮点数的二进制存储方式,我们知道,计算机仅仅可以使用二进制无限的接近部分浮点数,但是无法完全接近,即便64位浮点数以及可以很高精度的接近了,但是仍旧会产生误差.浮点数的算术运算仅仅可以产生一个近似值,这个近似值接近于真实值.
有一个比较悲观的事实就是,这些错误会随着一系列的计算而累加起来,从而导致偏差越来越多,结果越来越不精确.
举个例子,我们都知道
(x + y) + z = x + (y + z)
但是,这一点在计算机中,可不一定会成立.
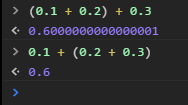
在部分计算机无法精确表达的浮点数产生的时候,就会导致误差的产生.
这种误差短期内还好,但是长期来说,是不可忍受的,假设是银行或者金融机构使用node作为服务端进行处理,日积月累,就会发生许多的问题.
浮点数运算是不准确的,那么我们应该怎么避免这个问题呢?
一个很简单的方法,就是避免浮点数的运算,把所有的运算都使用整型来进行.因为整型的运算是没有省略近似的.例如,上面那个例子,我们换成这个
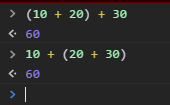
如果使用整型来进行算术运算,就不会产生上面的问题了,从而也保证了运算的精确性.
总结
- Javascript的数字类型是双精度浮点型.
- 在Javascript中,整型是double的一个子集,而不是一个独立的数据类型.
- Javascript在进行位运算的时候会把数字转换成32位整型来进行处理.
- 浮点数运算是不准确的,拥有许多的局限性.





网友评论