We begin with the simplest situation,a sun and a single planet,and investigate a few of the properties of this model solar system.
solar system.gif
solar system.gif
According to Newton's law of gravitation the magnitude of the force is given by
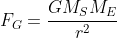
and we can obtain that:
Earth Orbiting the Sun
code1，as follows：
#coding:utf-8
import pylab as pl
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import animation
class circle():
def __init__(self,x0=1,y0=0,t0=0,vx0=0,vy0=2*math.pi,dt0=0.001,total_time=10):
self.x=[x0]
self.y=[y0]
self.vx=[vx0]
self.vy=[vy0]
self.R=x0**2+y0**2
self.t=[t0]
self.dt=dt0
self.T=total_time
def run(self):
for i in range(int(self.T/self.dt)):
vx=self.vx[-1]-(4*math.pi**2*self.x[-1]/self.R**2)*self.dt
vy=self.vy[-1]-(4*math.pi**2*self.y[-1]/self.R**2)*self.dt
self.vx.append(vx)
self.vy.append(vy)
self.x.append(self.vx[-1] * self.dt + self.x[-1])
self.y.append(self.vy[-1] * self.dt + self.y[-1])
def show(self):
pl.plot(self.x, self.y, '-', label='tra')
pl.xlabel('x(AU)')
pl.ylabel('y(AU)')
pl.title('Earth orbiting the Sun')
pl.xlim(-1.2,1.2)
pl.ylim(-1.2,1.2)
pl.axis('equal')
pl.show()
a=circle()
a.run()
a.show()
we can use the animation of matplotlib to gain the cartoon,
add follow codes:
def drawtrajectory(self):
fig=plt.figure()
ax = plt.axes(title=('Earth orbiting the Sun'),
aspect='equal', autoscale_on=False,
xlim=(-1.1, 1.1), ylim=(-1.1, 1.1),
xlabel=('x'),ylabel=('y'))
line=ax.plot([],[],'b')
point=ax.plot([],[],'ro',markersize=10)
images=[]
def init():
line=ax.plot([],[],'b',markersize=8)
point=ax.plot([],[],'ro',markersize=10)
return line,point
def anmi(i):
ax.clear()
line=ax.plot(self.x[0:10*i],self.y[0:10*i],'b',markersize=8)
point=ax.plot(self.x[10*i-1:10*i],self.y[10*i-1:10*i],'ro',markersize=10)
return line,point
anmi=animation.FuncAnimation(fig,anmi,init_func=init,frames=10000,interval=1,
blit=False,repeat=False)
we get follow gif
Earth Orbiting the Sun
If we consider the reduced mass
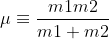
The orbital trajectory for a body of reduced mass is given in polar coordinates by
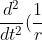+\frac{1}{r}=-\frac{\mu r2}{L2} F(r))
consider
Beta=3.0 t=0.3yr v=1.7pi.png
Beta=2.5，t=1.5yr,v=1.7pi.png
Beta=2.3,t=10yr,v=1.7pi.png
code
#coding:utf-8
import pylab as pl
import numpy as np
import math
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
from matplotlib import animation
class circle():
def __init__(self,x0=1,y0=0,t0=0,vx0=0,vy0=1.7*math.pi,dt0=0.001,Beta=2.3,total_time=10):
self.x=[x0]
self.y=[y0]
self.vx=[vx0]
self.vy=[vy0]
self.t=[t0]
self.dt=dt0
self.T=total_time
self.beta=Beta
def run(self):
for i in range(int(self.T/self.dt)):
R=(self.x[-1]**2+self.y[-1]**2)**0.5
vx=self.vx[-1]-(4*math.pi**2*self.x[-1]/R**(self.beta+1))*self.dt
vy=self.vy[-1]-(4*math.pi**2*self.y[-1]/R**(self.beta+1))*self.dt
self.vx.append(vx)
self.vy.append(vy)
self.x.append(self.vx[-1] * self.dt + self.x[-1])
self.y.append(self.vy[-1] * self.dt + self.y[-1])
def show(self):
pl.plot(self.x, self.y, '-', label='tra')
pl.xlabel('x(AU)')
pl.ylabel('y(AU)')
pl.title('Earth orbiting the Sun')
pl.xlim(-1,1)
pl.ylim(-1,1)
pl.axis('equal')
pl.show()
def drawtrajectory(self):
fig=plt.figure()
ax = plt.axes(title=('Earth orbiting the Sun '),
aspect='equal', autoscale_on=False,
xlim=(-1.1, 1.1), ylim=(-1.1, 1.1),
xlabel=('x'),ylabel=('y'))
line=ax.plot([],[],'b')
point=ax.plot([],[],'ro',markersize=10)
images=[]
def init():
line=ax.plot([],[],'b',markersize=8)
point=ax.plot([],[],'ro',markersize=10)
return line,point
def anmi(i):
ax.clear()
line=ax.plot(self.x[0:10*i],self.y[0:10*i],'b',markersize=8)
point=ax.plot(self.x[10*i-1:10*i],self.y[10*i-1:10*i],'ro',markersize=10)
return line,point
anmi=animation.FuncAnimation(fig,anmi,init_func=init,frames=100000,interval=1,
blit=False,repeat=False)
plt.show()
a=circle()
a.run()
a.show()
#a.drawtrajectory()
then we get the animation
Beta=3.0,v=2.0pi,t=200yr
for the problem 4.8， I use the follow code to calculate
import pylab as pl
import numpy as np
import math
class circle():
def __init__(self,x0=0.72,y0=0,t0=0,vx0=0,dt0=0.001,Beta=2.0,total_time=10,e0=0.007):
self.x=[x0]
self.y=[y0]
self.vx=[vx0]
self.vy=[]
self.t=[t0]
self.dt=dt0
self.T=total_time
self.beta=Beta
self.e=e0
def run(self):
vy0=2*math.pi*(1-self.e)/math.sqrt(1+self.e)
self.vy.append(vy0)
for i in range(int(self.T/self.dt)):
R=(self.x[-1]**2+self.y[-1]**2)**0.5
vx=self.vx[-1]-(4*math.pi**2*self.x[-1]/R**(self.beta+1))*self.dt
vy=self.vy[-1]-(4*math.pi**2*self.y[-1]/R**(self.beta+1))*self.dt
self.vx.append(vx)
self.vy.append(vy)
self.x.append(self.vx[-1] * self.dt + self.x[-1])
self.y.append(self.vy[-1] * self.dt + self.y[-1])
self.t.append(self.t[-1]+self.dt)
if(self.y[-1]<0):
a=(self.x[0]-self.x[-1])/2
T=2*self.t[-1]
k=T**2/a**3
break
print(k)
a=circle()
a.run()
网友评论