这篇文章就简单讲一个例子，希望大家动手做一个demo，这样来体会这个库的使用方式。
理论部分
不知道大家还记不记得g2o的经典demo，sphere.我们今天就来自己用ceres做一个图优化，从而学会ceres的使用。李群李代数基本功我不想在这里太多的讲解，就给大家简单的把公式推导一下，然后上代码(这个误差定义未必好，想做的更好的朋友可以考虑用更好的误差定义，从而有更好的线性化策略)，废话不多说，直接上公式，为了简略起见，我就不去写那个hat和vee符号了，相信大多数朋友对这套玩意儿早已烂熟于心
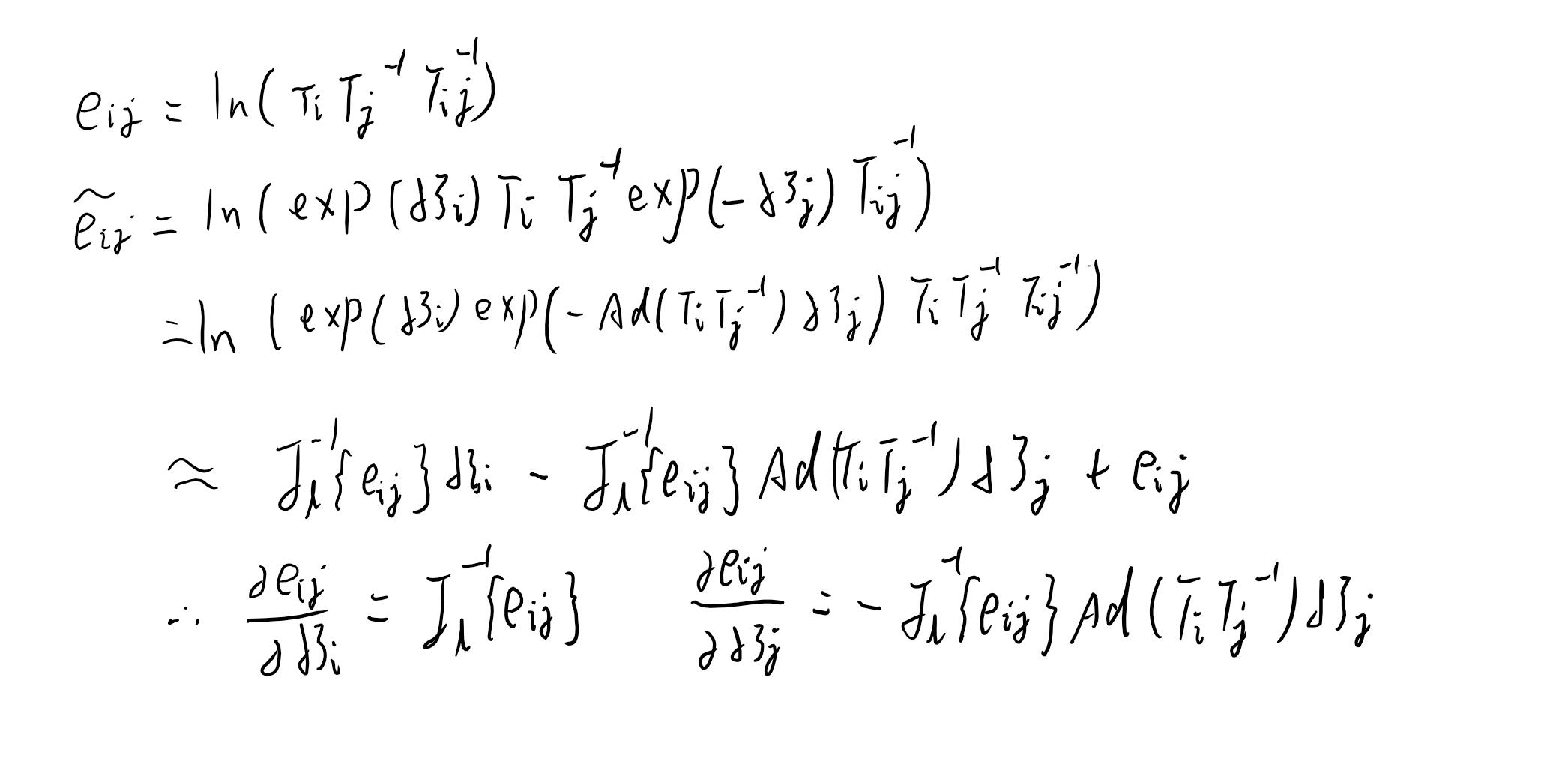sphere.jpg-87.8kB
如上图，最后就这样得到了线性化结果，然后你就可以拿去定义g2o的边了，不过这不是今天的重点，接下来我们来用ceres写图优化
ceres-solver使用
这个程序我已经上传到我的github上，没怎么去考虑程序设计，这个程序附带显示端，私以为做个仿真应该还是可以了，记得给一个星星哦，网址为:https://github.com/Lancelot899/g2o_sphere
同时还有一个ceres写得pnp的仿真，程序和这个程序也类似，只有雅可比计算有一些不同，大家有兴趣也可以看看https://github.com/Lancelot899/ceres_pnp
废话不多说，进入程序编写部分，首先大家可以在我的github上把这个程序下载下来，外围的数据读取显示等都已完成，优化的核心代码在Sphere.cpp文件中，首先我先介绍一下需要打交道的数据结构，这部分代码在DataStruct.h文件中
struct Vertex {
int index;
Eigen::Matrix<double, 6, 1> pose;
};
struct Edge {
int i;
int j;
Sophus::SE3d pose;
Eigen::Matrix<double, 6, 6> infomation;
};
点数据结构里面有点的索引，以及表示位姿的李代数的值，边数据结构存储了边连接的点的索引，以及边的约束(SE3)，还有信息矩阵，这些数据的读取和显示已经在程序的其他部分做好了
然后是Sphere.cpp文件，在这个文件中，大家可以重新定义误差，然后实现一个自己的优化。使用ceres做优化，首先要做的是定义损失函数，在官方网站上有很多可以定义损失函数的方法，在这里我选择了一个相对比较灵活的方式，即继承"ceres::SizedCostFunction"
这是个可变参数的模板，第一个参数为误差的维度，由于误差是SE(3)的李代数se(3)，所以是6维，后面的参数都是你要传入的参数的维度，这里要优化两个位姿，所以需要传入两个参数，每个位姿的维度为6，所以设置两个6，因此在程序中继承它的时候，传入了模板参数<6,6,6>，之后核心在于重载函数
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const;
注意这里是的const，一个不能少，我来介绍一下这个函数怎么写。
由于你有两个传入参数，所以parameters和jacobians这个二级指针里面，含有两个一级指针，就是说parameters[0]和parameters1,以及jacobians[0]和jacobians1这四个指针是有内存的，当然residuals也是有内存的
之后，由于param的维度都是6，所以parameters[0]和parameters1的空间分配量都为6,residuals自然也是6，注意，jacobians[0]和jacobians1两个雅可比指针的维度都是36,因为误差是6维,参数是6维,求导得到的矩阵为6*6，在这里把这个矩阵存成向量，行优先存储。你需要在这个函数里面把残差已经雅可比全部计算好，然后返回一个true
virtual bool Evaluate(double const* const* parameters,
double* residuals,
double** jacobians) const {
Eigen::Map<const Eigen::Matrix<double, 6, 1>> lie_i(*parameters);
Eigen::Map<const Eigen::Matrix<double, 6, 1>> lie_j(*(parameters + 1));
Eigen::Matrix<double, 6, 6> Jac_i;
Eigen::Matrix<double, 6, 6> Jac_j;
Sophus::SE3d T_i = Sophus::SE3d::exp(lie_i);
Sophus::SE3d T_j = Sophus::SE3d::exp(lie_j);
Sophus::SE3d Tij_estimate = T_i * T_j.inverse();
Sophus::SE3d err = Tij_estimate * T_ij_.inverse();
Eigen::Matrix<double, 6, 6> Jl;
Jl.block(3, 3, 3, 3) = Jl.block(0, 0, 3, 3) = Sophus::SO3d::hat(err.so3().log());
Jl.block(0, 3, 3, 3) = Sophus::SO3d::hat(err.translation());
Jl.block(3, 0, 3, 3) = Eigen::Matrix3d::Zero();
Eigen::Matrix<double, 6, 6> I = Eigen::Matrix<double, 6, 6>::Identity();
Jl.noalias() = sqrt_information_ * (I - 0.5 * Jl);
Jac_i = Jl;
Eigen::Matrix<double, 6, 1> err_ = sqrt_information_ * err.log();
const Eigen::Matrix<double, 3, 3>& R = Tij_estimate.rotationMatrix();
Eigen::Matrix<double, 6, 6> adj;
adj.block<3, 3>(3, 3) = adj.block<3, 3>(0, 0) = R;
adj.block<3, 3>(0, 3) = Sophus::SO3d::hat(Tij_estimate.translation()) * R;
adj.block<3, 3>(3, 0) = Eigen::Matrix<double, 3, 3>::Zero(3, 3);
Jac_j = -Jac_i * adj;
int k = 0;
for(int i = 0; i < 6; i++) {
residuals[i] = err_(i);
if(jacobians) {
for (int j = 0; j < 6; ++j) {
if (jacobians[0])
jacobians[0][k] = Jac_i(i, j);
if (jacobians[1])
jacobians[1][k] = Jac_j(i, j);
k++;
}
}
}
return true;
}
这段代码应该能和上面的公式都对上，应该说明的两个地方为sqrt_information_，由于整个误差计算是有信息矩阵的，你需要把信息矩阵分解一下，然后乘到雅可比上，最后得到不带权值的最小二乘法，简单用公式说明就是:
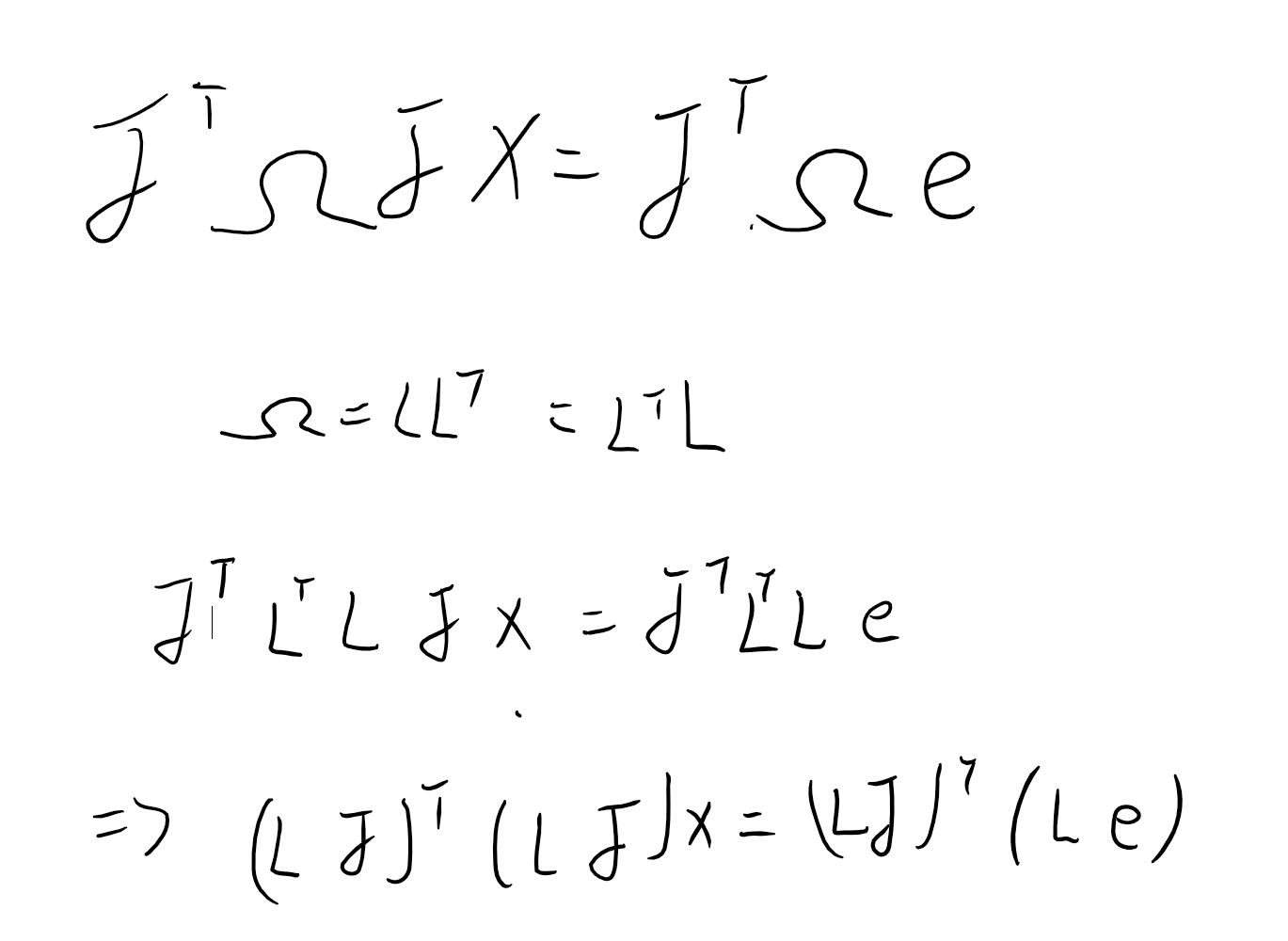sphereLL.jpg-42.3kB
所以大家可以看到我在构造函数里面把这个事做了，然后后面直接乘一下雅可比得到新的最小二乘法。
Eigen::LLT<Eigen::Matrix<double, 6, 6>> llt(information);
sqrt_information_ = llt.matrixL();
之后，由于大家都知道，点里面的位姿是李代数，所以更新的时候是不能够线性相加的，而要用这样那样的公式：
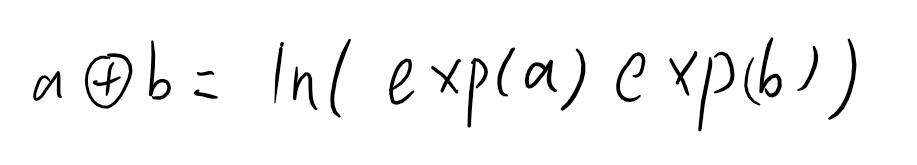lie.jpg-10.6kB
因此你需要自己设置更新方法，这个就是使用本地化参数了，需要继承" ceres::LocalParameterization"这个类，实现四个接口，分别是:
virtual bool Plus(const double* x,
const double* delta,
double* x_plus_delta) const;
virtual bool ComputeJacobian(const double* x,
double* jacobian) const;
virtual int GlobalSize() const;
virtual int LocalSize() const ;
在我的程序里面，雅可比都在前面全部搞定了，也没有本地参数(你实际上要用的)和全局参数(最小二乘法算的)参数的变化，所以你会看到ComputeJacobian这个函数，我就设置了个单位矩阵上去，然后实现了Plus这个函数
做好这些事，你的准备工作就算全部写好了，最后就是设置求解器,都是套路活儿，代码是死的，大家看看我写的应该就会了，就写这么多，有什么问题，可以私下与我联系
网友评论