这节进入逻辑回归。逻辑回归实际上是一个分类问题,很多情况下,我们的输出值y并不是一个连续量,很可能只是0、1这样的离散量。我们可能用1表示一种输出类型,用0表示另一种输出类型,显然此时不能像之前那样直接利用线性回归来判定我们的数据趋势。
<h4>Sigmoid Function</h4>
在这种情况下,我们先在数学上表示y的范围:

其次:
\le1)
我们将认为大于0.5的值认定为逻辑1,小于0.5的值认定为逻辑0,因此我们需要找到一个函数满足上面的关系,在这里我们使用sigmoid function,它同时也被称为logistic function:

实际上h(x)的数值代表的是输出值为1的概率,就像上面这个推导式,h(x)≥0.5的意思指的是y=1的概率大于百分之五十,用数学表达式表示则为:

=%5Cfrac%7B1%7D%7B2m%7D%5Csum_%7Bi=1%7D%5E%7Bm%7D%5Bh_%7B%5Ctheta%7D%5Cleft(%20x%5Ei%20%5Cright)-y%5E%7B(i)%7D%5D%5E2=%5Cfrac%7B1%7D%7B2m%7D(X%5Ctheta%20-%20%5Cvec%7By%7D)%5ET(X%5Ctheta%20-%20%5Cvec%7By%7D))
显然对于分类问题,这样的cost function是不合理的,因此我们可以构造一个函数来合理地描述分类问题的偏差值。
令:

根据上面的条件,我们可以构造一个函数,如下所示:

为了计算方便,我们将上面的式子简化为:

所以逻辑回归的cost function为:

将上面的式子向量化后得到:
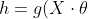)

利用梯度下降算法我们可以得到参数的变化方程:
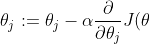)
为了方便下面对cost function求偏导,我们先计算sigmoid function的导数:

然后求代价函数的偏导数:

(对,很长...近乎绝望...但是并不难)
因此,对代价函数的偏导向量化之后得到:
=\frac{1}{m}X^T [g(X \theta)-\vec{y}\ ])
<h4>最后</h4>
这一节的数学推导可能略难一点,请好好消化,如果有不明白的地方多去问问度娘==
下一节就用matlab实现上述算法。





网友评论