停下来思考下神经网络

前面介绍了一个简单的神经网络，用来解决了一个非常简单的模型，文章链接

输入1	输入2	输入3	输出
0	0	1	0
0	1	1	1
1	0	1	1
1	1	1	0

那本节主要是对神经网络的一点思考

1. 优化

在神经网络中backpropagation是非常重要的一个算法，backpropagation能帮助我们测量出每个weight对于最终输出错误的影响。

Backpropagation allowed us to measure how each weight in the network contributed to the overall error.

测量出每个weight对于最终error的影响后，下一步就是想着怎么去更新这些weight了，最终目标是使得error最小，至于这些更新的算法就有很多了，有：
• Annealing
• Stochastic Gradient Descent
• AW-SGD (new!)
• Momentum (SGD)
• Nesterov Momentum (SGD)
• AdaGrad
• AdaDelta
• ADAM
• BFGS
• LBFGS

每个算法都是侧重某一个点做的优化，没有什么万能算法，不过有一点是我们都需要知道的：

有了算法，在运用到实际的过程中，我们都需要去 tuning。

谈到tuning就不由想到之前听精英日课里讲到的物理学中的「微调（fine tuning）」，里面说我们的宇宙就像是被人精心微调过似的，像一些关键的物理学公式中的参数，目前都是我们测量出来的，那谁规定这些参数就必须是这样子的呢？如果不是这样子，似乎宇宙就不稳定了，这让我不由想到，现在的神经网络，其模型是越来越复杂，里面需要调优的参数也越来越多，我们也无法去解释这些参数为什么是这个样子的，一切都是计算出来的，目前复杂的网络已经不是人能理解的了，如果宇宙也是通过一个复杂的网络产生的，那我们目前发现的所有规律，可能只是这个网络中的一部分，我们所有的一些测量出来的常量就是神经网络的中的weight，我们会与解释为什么参数是这样子吗？显然不可能，因为所有的参数都是通过输入输出网络自己“学习”出来的！
那可能物理学目前所有的一些公式都只是整个大系统中的一小部分，我们如果不解决系统最初的输入和输出是什么，不可能真正的了解系统，所有的努力只是其中的某一层网络之间的关系而已！

扯远了，回到我们的梯度下降。

2.Gradient Descent

我们看图：

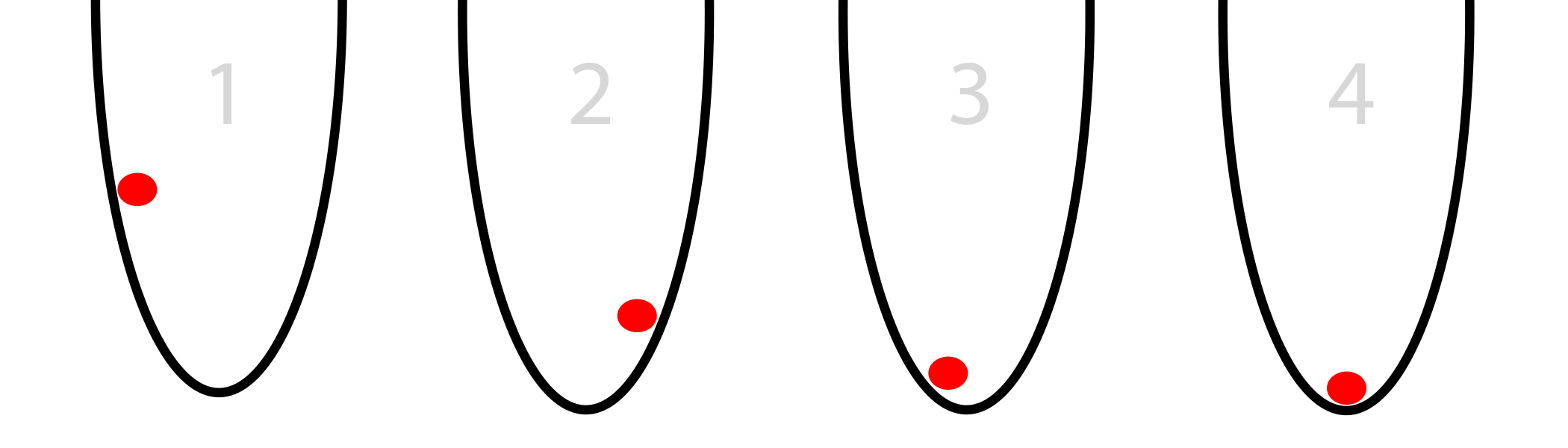
图中的球不断的滚动，最终就会下降到最地点，那球怎么知道要往哪走呢？

人往高处走，水往低处流，球自然往稳定的地方走。

球在移动的过程中，唯一知道的信息就是当时的斜度（slope），如下图：

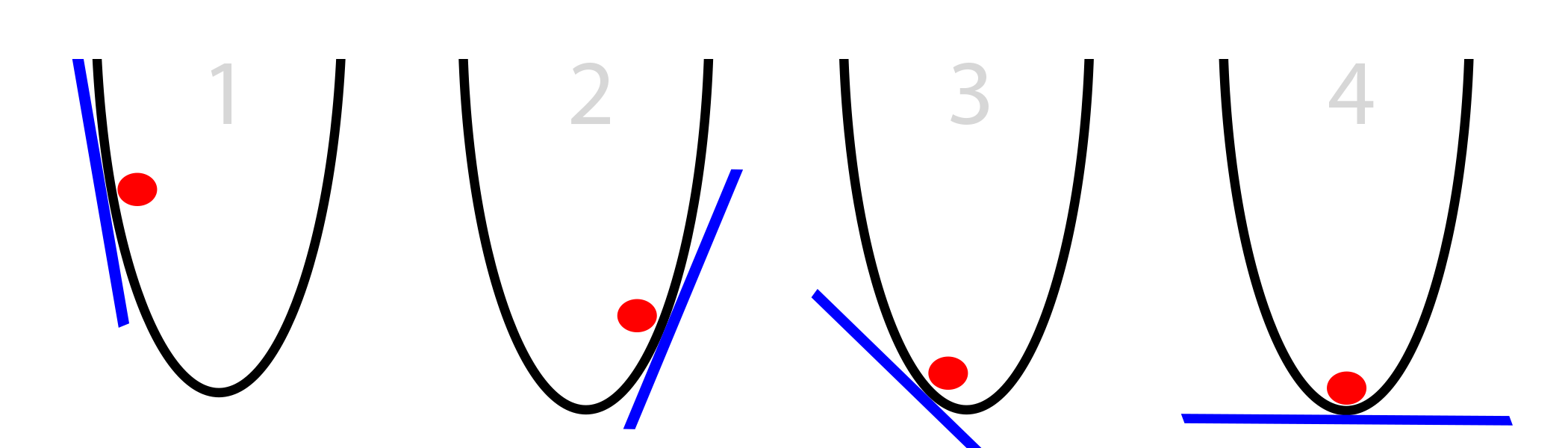
我们简单的描述下球移动的整个过程：

1. 计算当前小球所在点的斜度
2. 如果斜度为负，往右走
3. 如果斜度为正，往左右
4. 重复直到斜度为0

解决了小球走向的问题，下一步就是到底走多远的问题，一个简单的方案就是每次都走斜度距离，用数学公式来描述就是：

$$
x = x - slope
$$

现在我们知道了球往哪走，每次走多少，那按照这个规则来走，理论上球最后就能到达底部了。

3.But....球有时候也会凌乱

以上描述的算法也不是万能的，有时候球也会凌乱，走不到底部。

3.1 问题1.当斜率太大

看图：

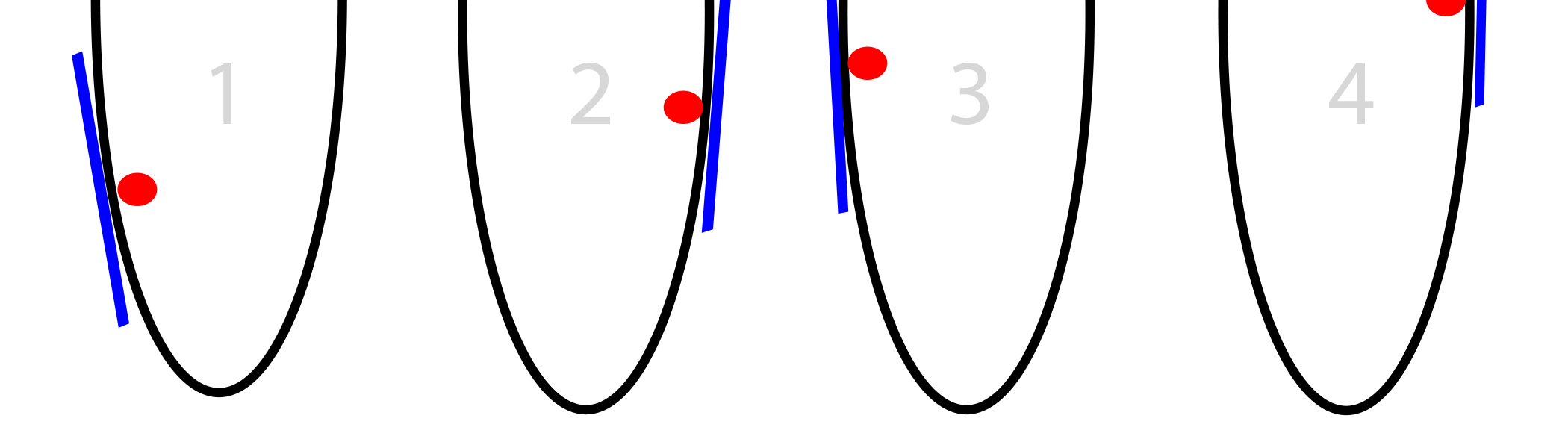
有时候，当斜度太大的时候，每次球都从一个高出走向另一个方向的更高处，导致越来越偏离，也就是所谓的发散，那怎么解决的呢？
一个显然的做法就是减少每次移动的幅度，数学描述就是

$$
x = x - (alpha*slope)
$$

此处alpha是一个0-1之间的数，通过这种方法，我们就能慢慢的到达底部了。

3.2 问题2.局部最小

看图：

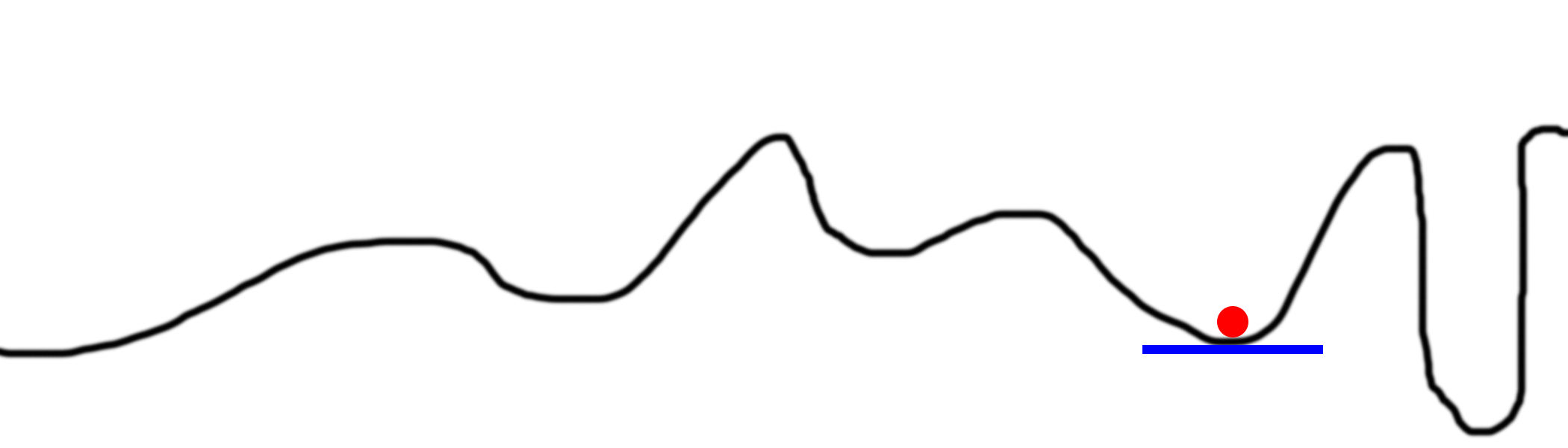
有时候我们有多个低洼处，怎么办呢？方法也很简单，我们随机的放多个球，看哪个球到达的底部最低，如下图：

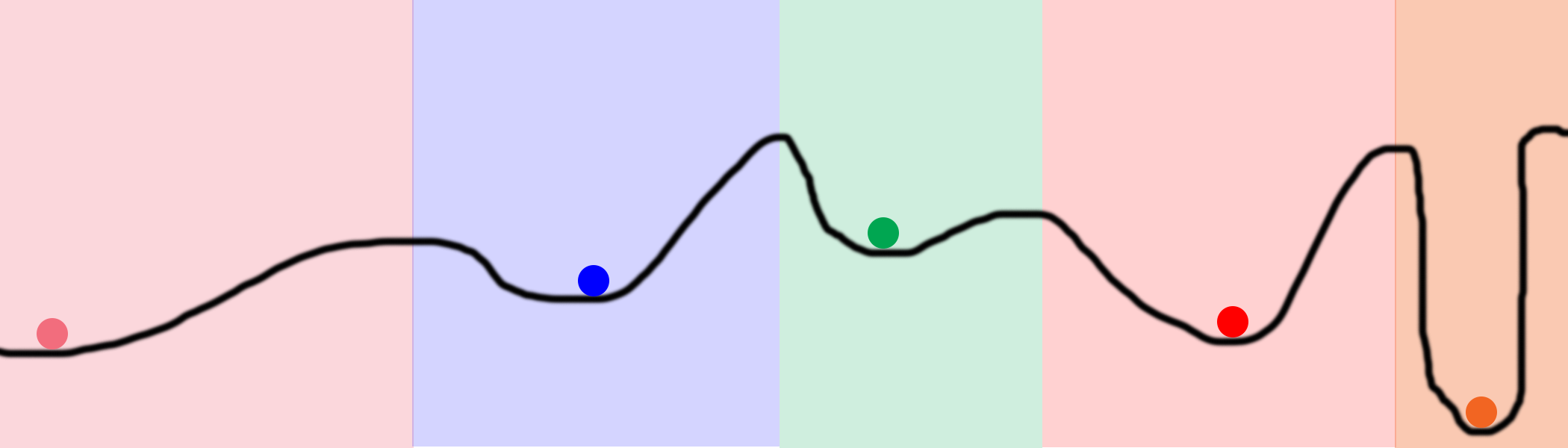
那在神经网络中，怎么能够达到上述的效果呢？
神经网络中，这是通过增加层数实现的，每个隐藏的node其初始状态都是随机的，这种通过调节hidden node大小的方法，能够让我们尽可能的遍历所有的空间，找到其中最优的值。

讨论.在上图中，我们随机放了好多小球，最后所有的小球都停在了5个地点，那问题是：我们为什么要浪费那么多计算资源来重复计算呢？最后这些小球会到达同一个地方？一个优化显然就是对于那些同样结果的小球，我们就赶紧听下他，这样就能尽可能的减少资源的浪费！

3.3 问题3.当斜率太小

问题1是斜率太大，如果太小呢？

上图我们会发现我们红色的小球走着走着就会卡住！😳一脸懵逼了。
如果我们每次移动的步长太小，那结果就是异步小心调入了一个小凹槽，再也出不来了！
再来看一个图：

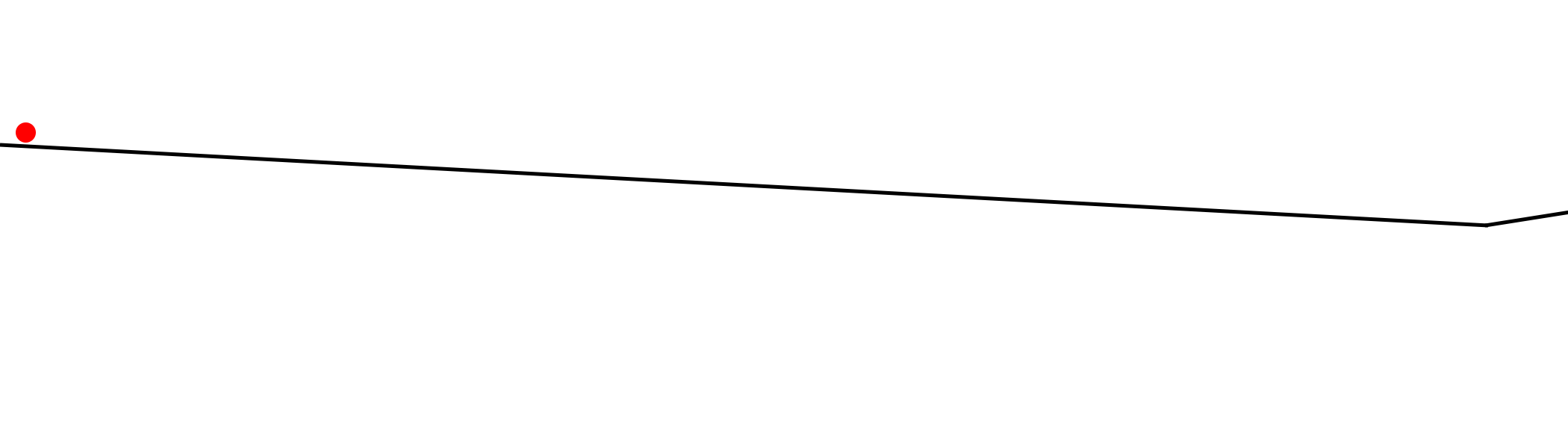
即使我们没有小凹槽，但是如果步长太小的话，我们也会耗费好长时间才能到达底部

4. 随机梯度下降（SGD）

还是看图，图中这条曲线代表什么？
首先，我们必须要知道在神经网络中，我们都在试着最小化error with respect to the weights
所以上面的曲线含义是：随着一个单子的weight变化，error的变化，这么说可能还是不太好理解，可以看线性回归背后的数学，这里的曲线就是固定住其他weight，单独变化一个weight的曲线。

以上就是目前关于神经网络的所有思考。待继续。。。

以上内容参考了：A Neural Network in 13 lines of Python (Part 2 - Gradient Descent)