在一个没有任何电荷的无限大空间中,电势的分布遵循Laplace's equation:
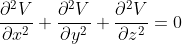
接下来的讨论中,我们将针对拉普拉斯方程展开讨论,并将其用python代码模拟出来。
公式推导
在点(i,j,k)上我们对x的偏分可以写作:
-v(i,j,k)}{\Delta x})
或者:
-V(i-1,j,k)}{\Delta x})
因此,容易得到:
-V(i,j,k)}{\Delta x}-\frac{V(i,j,k)-V(i-1,j,k)}{\Delta x}])
再稍微做一点运算,得到:
+V(i-1,j,k)-2V(i,j,k)}{(\Delta x)^2})
对y,z方向上的偏分运算也是类似的,在此就不做推导,再将上面的式子代入Laplace's equation中,得到:
=\frac{1}{6}[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)+V(i,j,k+1)+V(i.j,k-1)])
我们先考虑平面的情况,因此上式改为:
=\frac{1}{4}[V(i+1,j,k)+V(i-1,j,k)+V(i,j+1,k)+V(i,j-1,k)])
具体算法
我们首先预设一些初始值,并用上式不断的迭代这些值,直到这些值满足Laplace's equation
- set initial value of laplace's V to be zero.
- loop through all points(i,j) except the boundary,where values of V_n are fixed by the boundary conditions.
-

三维图


电场分布

假设在无限大平面上有两块电势分别为1和-1的平板,试作出这个体系的电势图和电场分布



总结
总的来说,这道题目的算法并不复杂,难的地方可能在python值传递、浅copy和深copy的问题上,与其花大量时间研究python的内部机制,倒不如直接用numpy中的矩阵进行计算,也能大大简化代码。
致谢
绘图部分的代码参考了华杨学姐的代码
-












网友评论