CS229_5-局部加权线性回归

---

局部加权线性回归

欠拟合与过拟合

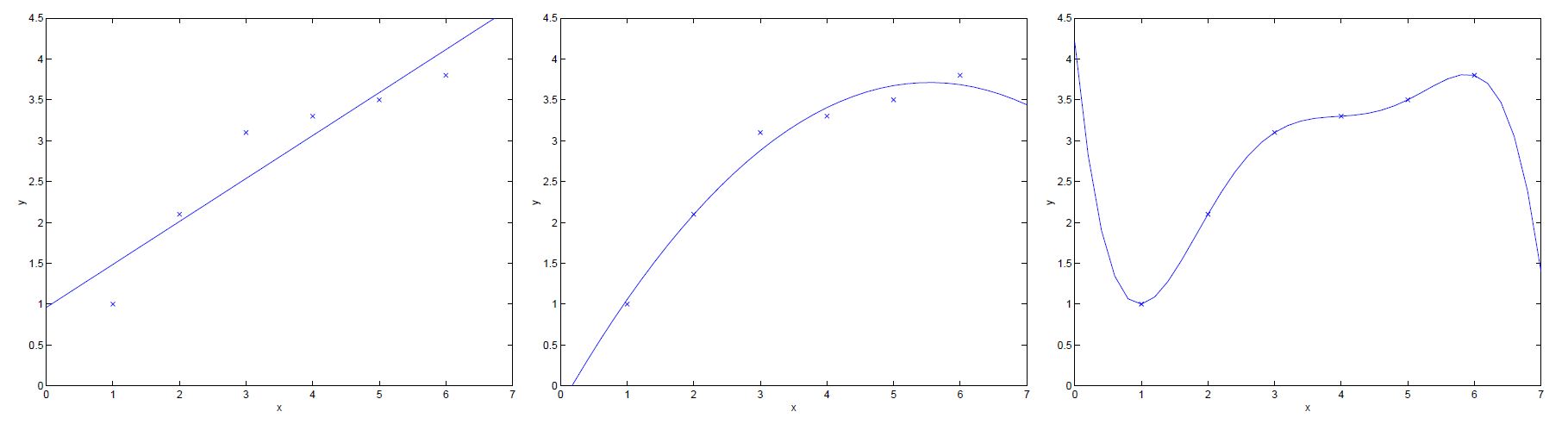
上述三幅图展示了，不同假设函数对于同一训练集的拟合情况。

• 左图：假设函数为。很明显可看出，其拟合情况不太理想，我们将这种情况称为欠拟合（under-fitting）；
• 右图：假设函数为。很明显可看出，其拟合情况太好了，以至于其可能对于一些训练集外的数据点无法做到很好地预测，因此我们将这种情况称为过拟合（over-fitting）。

因此，我们在设计假设函数时，不能过分地追求对训练集的拟合程度，只需其拟合程度达到上述图中中间图的拟合程度即可。

补充：给定一个假设空间，一个假设属于，如果存在其他的假设，使得在训练样例上的错误率比好，但在整个个实例分布上的错误率比小，那么就说假设出现过拟合的情况。欠拟合的定义与之相似。^[1]

局部加权线性回归算法

局部加权线性回归（Locally Weight Linear Regression，LWR）算法顾名思义为线性回归算法的扩展，当目标假设为线性模型时，因此我们采用线性回归；但如果目标假设不是线性模型，比如一个忽上忽下的的函数，这时用线性模型就拟合的很差。为了解决这个问题，当我们在预测一个点的值时，我们选择和这个点相近的点而不是全部的点做线性回归。基于这个思想，就有了局部加权回归算法。

原始线性回归算法：

1. 找到参数使其最小化；
2. 输出。

局部加权线性回归算法：

1. 找到参数使其最小化；
2. 输出。

两者相互比较可知，在最小化时，局部加权线性回归算法添加了权值。其作用为根据要预测的点与数据集中的点的距离来为训练集中的点赋予权值，当某点距离待预测点较远时，其权重较小；反之则权重较大。

其中，参数称为波长参数，其控制权值随距离增大而下降的速率。

注：若为向量，则权值将改写为：

或者为：

补充：

• 参数学习算法（Parametric Learning Algorithm）是一类有固定数目参数的用来进行数据拟合的算法，线性回归算法即为此类；
• 非参数学习算法（Non-Parametric Learning Algorithm）是一类参数数量随训练集增大而增加的算法，局部加权线性回归算法即为此类。

---

1. http://blog.csdn.net/stdcoutzyx/article/details/9113681 ↩