1、决策树算法

决策树(decision tree)又叫判定树，是基于树结构对样本属性进行分类的分类算法。以二分类为例，当对某个问题进行决策时，会进行一系列的判断或者“子决策”，将每个判定问题可以简单理解为“开”或“关”，当达到一定条件的时候，就进行“开”或“关”的操作，操作就是对决策树的这个问题进行的测试。所有的“子决策”都完成的时候，就构建出了一颗完整的决策树。

一颗典型的决策树包括根结点、若干个内部结点和若干个叶结点；叶结点对应着决策结果，其它每个结点对应于一个属性测试；每个结点包含的样本集合根据属性测试的结果被划分到子结点中；根结点包含样本全集。

决策树学习的目的在于产生一颗泛化能力强，即处理未见示例能力强的决策树，基本流程遵循简单直观的“分而治之”(divide-and-conquer)策略。

一般而言，随着划分过程的不断进行，我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即结点的“纯度”(purity)越来越高。

• 信息熵(information entropy)

  信息熵是度量样本集合纯度最常用的一种指标。在样本集合D中，第k 类样本所占比例为 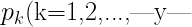)则D的信息熵为：=-\sum_{k=1}^{|y|}p_klog_2p_k $$)

  Ent(D)的值越小，D的纯度越高。

• 信息增益(information gain)

  离散属性a中有V个可能取值使用a对样本集D进行划分，则产生V个分支结点，其中第v个分支结点包含了D中所有在属性a上取值为a^v的样本，记作D^v，D^v信息熵即为Ent(D^v)

  考虑到不同分支结点包含样本数不同，则给分支结点赋权最后可计算出属性a对样本集D进行划分所得到的信息增益：=Ent(D)-\sum_{v=1}^{V}\frac{|Dv|}{|D|}Ent(D^v)$$)

  著名的ID3算法就是基于信息增益构建的。

  一般信息增益越大，则意味使用属性a进行划分所获得的“纯度提升”越大。

• 信息增益率(gain ratio)

  信息增益准则对可数数目较多属性有所偏好。这里考虑一个特殊情况，若分支数目就为样本数，则信息增益就为样本集信息熵，此时信息增益亦越大，此时决策树并不具有泛化能力，无法对新样本进行有效预测。

  信息增益率就是为了解决上述问题而产生的。信息增益率的计算公式为：=\frac{Gain(D,a)}{IV(a)} $$)其中=-\sum_{v=1}^V \frac{|D^{v|}{|D|}log_2\frac{|D}v|}{|D|} $$)称为属性a的“固有值”(intrinsic value)，属性a的可能取值数目越多（即V越大），则IV(a)通常会越大。

  基于ID3算法改进的C4.5算法就是基于信息增益率构建的。

  需要注意的是，信息增益率对于可取值数目较少的属性有所偏好。

• 基尼指数(gini index)

  基尼指数是常用于CART决策树的一种划分准则，样本集D的“纯度”也可通过这个指数进行确定。基尼指数：=\sum_{k=1}^{|y|}\sum_{k{'}\neq{k}}p_kp_{k^{{'}}=1-\sum_{k=1}}{|y|}p_k^2 $$)

  它反映了从样本集D中随机抽取两个样本，其类别标记不一致的概率。

  因此Gini(D)越小，样本集D纯度越高。

  定义属性a的基尼指数为：=\sum_{v=1}^{{|V|}\frac{|D}v|}{|D|}Gini(D^v) $$)在候选属性集合A中，选择使得划分后基尼指数最小的属性做为最优划分属性。

2、算法实现

本文采用以下样本集(data.txt)实现决策树

编号	色泽	根蒂	敲声	纹理	脐部	触感	好瓜
1	青绿	蜷缩	浊响	清晰	凹陷	硬滑	是
2	乌黑	蜷缩	沉闷	清晰	凹陷	硬滑	是
3	乌黑	蜷缩	浊响	清晰	凹陷	硬滑	是
4	青绿	蜷缩	沉闷	清晰	凹陷	硬滑	是
5	浅白	蜷缩	浊响	清晰	凹陷	硬滑	是
6	青绿	稍蜷	浊响	清晰	稍凹	软粘	是
7	乌黑	稍蜷	浊响	稍糊	稍凹	软粘	是
8	乌黑	稍蜷	浊响	清晰	稍凹	硬滑	是
9	乌黑	稍蜷	沉闷	稍糊	稍凹	硬滑	否
10	青绿	硬挺	清脆	清晰	平坦	软粘	否
11	浅白	硬挺	清脆	模糊	平坦	硬滑	否
12	浅白	蜷缩	浊响	模糊	平坦	软粘	否
13	青绿	稍蜷	浊响	稍糊	凹陷	硬滑	否
14	浅白	稍蜷	沉闷	稍糊	凹陷	硬滑	否
15	乌黑	稍蜷	浊响	清晰	稍凹	软粘	否
16	浅白	蜷缩	浊响	模糊	平坦	硬滑	否
17	青绿	蜷缩	沉闷	稍糊	稍凹	硬滑	否

通过以下代码导入样本集数据

import pandas as pd#导入pandas库
import numpy as np#导入numpy库

data = pd.read_csv('data.txt', '\t', index_col='编号')
labels = list(data.columns)
dataSet = np.array(data).tolist()#处理读入数据为list类型，方便后续计算

2.1、计算信息熵

导入样本集，通过下面代码实现根结点信息熵的计算

from math import log

def calcShannonEnt(dataSet):
    numEntries = len(dataSet)#计算样本集的总样本数量
    labelCounts = {}#设置一个空的dict类型变量
    for featVec in dataSet:#遍历每行样本集
        currentLabel = featVec[-1]#选取样本集最后一列，设置为labelCounts变量的key值
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0#key对应value初始化
        labelCounts[currentLabel] += 1#累计value，即计算同类别样本数
    shannonEnt = 0.0#初始化信息熵
    for key in labelCounts:
        prob = float(labelCounts[key]) / numEntries#计算频率
        shannonEnt -= prob * log(prob, 2)#计算信息熵
    return shannonEnt

print(calcShannonEnt(dataSet))

0.9975025463691153

可以得到是否“好瓜”，即根结点的信息熵为0.9975025463691153

判断是否“好瓜”的有｛色泽，根蒂，敲声，纹理，脐部，触感｝等6个子属性，同时以“色泽”属性为例，它有3个可能取值｛青绿，乌黑，浅白｝，分别记为D¹(色泽=青绿)、D²(色泽=乌黑)和D¹(色泽=浅白)。
如果希望通过上面计算根结点的代码计算不同子属性信息熵，这里就需要对样本集进行划分，选择相应的子属性。这里通过下面的代码实现样本集的划分。

def splitDataSet(dataSet, axis, value):
    #dataSet为样本集
    #axis为子属性下标，如0代表子属性“色泽”
    #value为上述子属性取值
    retDataSet = []
    for featVec in dataSet:
        if featVec[axis] == value:
            reducedFeatVec = featVec[:axis]
            reducedFeatVec.extend(featVec[axis + 1:])
            retDataSet.append(reducedFeatVec)
    return retDataSet

newdataSet1=splitDataSet(dataSet, 0, '青绿')#将为“青绿”的样本集合划分出来

[['蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], ['蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'], ['稍蜷', '浊响', '清晰', '稍凹', '软粘', '是'], ['硬挺', '清脆', '清晰', '平坦', '软粘', '否'], ['稍蜷', '浊响', '稍糊', '凹陷', '硬滑', '否'], ['蜷缩', '沉闷', '稍糊', '稍凹', '硬滑', '否']]

newdataSet2=splitDataSet(dataSet, 0, '乌黑')#将为“青绿”的样本集合划分出来

[['蜷缩', '沉闷', '清晰', '凹陷', '硬滑', '是'], ['蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], ['稍蜷', '浊响', '稍糊', '稍凹', '软粘', '是'], ['稍蜷', '浊响', '清晰', '稍凹', '硬滑', '是'], ['稍蜷', '沉闷', '稍糊', '稍凹', '硬滑', '否'], ['稍蜷', '浊响', '清晰', '稍凹', '软粘', '否']]

newdataSet3=splitDataSet(dataSet, 0, '浅白')#将为“青绿”的样本集合划分出来

[['蜷缩', '浊响', '清晰', '凹陷', '硬滑', '是'], ['硬挺', '清脆', '模糊', '平坦', '硬滑', '否'], ['蜷缩', '浊响', '模糊', '平坦', '软粘', '否'], ['稍蜷', '沉闷', '稍糊', '凹陷', '硬滑', '否'], ['蜷缩', '浊响', '模糊', '平坦', '硬滑', '否']]

由上面的划分可以看出“色泽=青绿”的正类为3/6，反类为3/6，“色泽=乌黑”的正类为4/6，反类为2/6，“色泽=浅白”的正类为1/5，反类为4/5。
通过上文代码计算每个取值的熵值：

print(calcShannonEnt(newdataSet1))
print(calcShannonEnt(newdataSet2))
print(calcShannonEnt(newdataSet3))

1.0
0.9182958340544896
0.7219280948873623

可以得到D¹(色泽=青绿)的信息熵为：1.0，D²(色泽=乌黑)的信息熵：为0.9182958340544896，D¹(色泽=浅白)的信息熵为：0.7219280948873623。

2.2、计算信息增益及最优划分属性选取

由下面的代码可以实现信息增益的计算

numFeatures = len(dataSet[0]) - 1#计算子属性的数量
baseEntropy = calcShannonEnt(dataSet)#计算根结点信息熵
columns=['色泽','根蒂','敲声','纹理','脐部','触感']#子属性
for i in range(numFeatures):
    featList = [example[i] for example in dataSet]
    uniqueVals = set(featList)
    newEntropy = 0.0
    for value in uniqueVals:
        #根据子属性及其取值划分样本子集
        subDataSet = splitDataSet(dataSet, i, value)
        prob = len(subDataSet) / float(len(dataSet))#权值
        newEntropy += prob * calcShannonEnt(subDataSet)
        print(value,'的信息熵为：',calcShannonEnt(subDataSet))#不同取值的信息熵
    infoGain = baseEntropy - newEntropy#计算信息增益
    print(columns[i],'信息增益为：',infoGain)
    print('----------------------------------')

青绿 的信息熵为： 1.0
乌黑 的信息熵为： 0.9182958340544896
浅白 的信息熵为： 0.7219280948873623
色泽 信息增益为： 0.10812516526536531
----------------------------------
蜷缩 的信息熵为： 0.9544340029249649
硬挺 的信息熵为： 0.0
稍蜷 的信息熵为： 0.9852281360342516
根蒂 信息增益为： 0.14267495956679288
----------------------------------
清脆 的信息熵为： 0.0
浊响 的信息熵为： 0.9709505944546686
沉闷 的信息熵为： 0.9709505944546686
敲声 信息增益为： 0.14078143361499584
----------------------------------
模糊 的信息熵为： 0.0
清晰 的信息熵为： 0.7642045065086203
稍糊 的信息熵为： 0.7219280948873623
纹理 信息增益为： 0.3805918973682686
----------------------------------
稍凹 的信息熵为： 1.0
平坦 的信息熵为： 0.0
凹陷 的信息熵为： 0.863120568566631
脐部 信息增益为： 0.28915878284167895
----------------------------------
硬滑 的信息熵为： 1.0
软粘 的信息熵为： 0.9709505944546686
触感 信息增益为： 0.006046489176565584
----------------------------------

一般某个子属性的信息增益越大，意味着使用该属性进行划分的“纯度提升”越大，下面通过改造上述代码，选取最优的划分属性。

# 基于信息增益选择最优划分属性
def chooseBestFeatureToSplit_Gain(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0#初始最优信息增益
    bestFeature = -1#初始最优子属性
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoGain):#选择最优子属性
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

chooseBestFeatureToSplit_Gain(dataSet)

3

上述结果表示在这个样本集中，最优的划分子属性是“纹理”，接下来根结点就通过该子属性进行划分。在该划分之后，通过剩余的其它子属性再进行信息增益的计算得到下个最优划分子属性，迭代进行，直到全部子属性变量完成。

2.3、基于信息增益率最优划分属性选取

计算信息增益率代码与上文计算信息增益的代码类似，同时下文基于该原则选择最优子属性的代码中有体现，这里不过多赘述。
同样的，基于信息增益率原则也是选择信息增益率最大的为最优划分结点，下面基于信息增益率划分最优子属性。
由于本文采用的样本集是离散型特征的样本，这里的信息增益率和基尼指数选择划分属性的实现并未针对连续型特征进行。后续会加以改进。

# 基于信息增益率选择最优划分属性
def chooseBestFeatureToSplit_GainRatio(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestGainRatio = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        iv = 0.0#初始化“固有值”
        GainRatio = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            iv -= prob * log(prob, 2)#计算每个子属性“固有值”
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        GainRatio = infoGain / iv#计算信息增益率
        if (GainRatio > bestGainRatio):#选择最优节点
            bestGainRatio = GainRatio
            bestFeature = i
    return bestFeature

chooseBestFeatureToSplit_GainRatio(dataSet)

3

上述结果表示在这个样本集中，最优的划分子属性同样是“纹理”，接下来的划分实现过程就由该结点开始。

2.4、计算基尼指数及最优划分属性选取

以下代码实现了基尼指数的计算。

# 计算基尼指数
def calcGini(dataSet):
    numEntries = len(dataSet)
    labelCounts = {}
    for featVec in dataSet:
        currentLabel = featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
        Gini = 1.0
        for key in labelCounts:
            prob = float(labelCounts[key]) / numEntries
            Gini -= prob * prob
    return Gini

calcGini(dataSet)#根结点基尼指数

0.49826989619377154

上述结果为根结点的基尼指数值。下面是通过基尼指数选择根结点的子结点代码实现。

# 基于基尼指数选择最优划分属性(只能对离散型特征进行处理)
def chooseBestFeatureToSplit_Gini(dataSet):
    numFeatures = len(dataSet[0]) - 1
    bestGini = 100000.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newGiniIndex = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet) / float(len(dataSet))
            newGiniIndex += prob * calcGini(subDataSet)
        if (newGiniIndex < bestGini):
            bestGini = newGiniIndex
            bestFeature = i
    return bestFeature

chooseBestFeatureToSplit_Gini(dataSet)

3

上述结果同样表示在这个样本集中，最优的划分子属性同样是“纹理”，接下来的划分实现过程也由该结点开始。

2.5、创建树

决策树的创建过程是迭代进行的，下面的代码是根据子属性的取值数目大小来进行每层根结点的选择的实现过程。即简单理解为选择“下一个根结点”。

import operator

# 选择下一个根结点
def majorityCnt(classList):
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0#初始化子属性取值的计数
        classCount[vote] += 1#累计
    #根据第二个域，即dict的value降序排序
    sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse = True)
    return sortedClassCount[0][0]#返回子属性取值

下面就是创建树的过程。

# 创建树
def createTree(dataSet, labels, chooseBestFeatureToSplit):
    classList = [example[-1] for example in dataSet]#初始化根结点
    if classList.count(classList[0]) == len(classList):#只存在一种取值情况
        return classList[0]
    if len(dataSet[0]) == 1:#样本集只存在一个样本情况
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)#最优划分属性选取
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel: {}}#初始化树
    del (labels[bestFeat])#删除已划分属性
    featValues = [example[bestFeat] for example in dataSet]#初始化下层根结点
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        #遍历实现树的创建
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels, chooseBestFeatureToSplit)
    return myTree

chooseBestFeatureToSplit=chooseBestFeatureToSplit_Gain#根据信息增益创建树
# chooseBestFeatureToSplit=chooseBestFeatureToSplit_GainRatio#根据信息增益率创建树
# chooseBestFeatureToSplit=chooseBestFeatureToSplit_Gini#根据基尼指数创建树
myTree = createTree(dataSet, labels, chooseBestFeatureToSplit)

myTree

{'纹理': {'模糊': '否',
  '清晰': {'根蒂': {'硬挺': '否',
    '稍蜷': {'色泽': {'乌黑': {'触感': {'硬滑': '是', '软粘': '否'}}, '青绿': '是'}},
    '蜷缩': '是'}},
  '稍糊': {'触感': {'硬滑': '否', '软粘': '是'}}}}

我们需要将划分好的决策树加载出来进行分类，这里定义一个分类的代码如下。

#分类测试器
def classify(inputTree, featLabels, testVec):
    firstStr = list(inputTree.keys())[0]
    secondDict = inputTree[firstStr]#下一层树
    featIndex = featLabels.index(firstStr)#将Labels标签转换为索引
    for key in secondDict.keys():
        if testVec[featIndex] == key:#判断是否为与分支节点相同，即向下探索子树
            if type(secondDict[key]).__name__ == 'dict':
                #递归实现
                classLabel = classify(secondDict[key], featLabels, testVec)
            else:
                classLabel = secondDict[key]
    return classLabel#返回判断结果

classify(myTree, ['色泽','根蒂','敲声','纹理','脐部','触感'],['乌黑','稍蜷','沉闷','稍糊','稍凹','硬滑'])

'否'#得到分类结果为'否'

由于决策树的训练是一件耗时的工作，当碰到较大的样本集的时候，为了下次使用的方便，这里将决策树保存起来。
这里通过pickle模块存储和加载决策树。

#保存树
def storeTree(inputTree,filename):
    import pickle
    fw = open(filename,'wb+')
    pickle.dump(inputTree,fw)
    fw.close()
 
#加载树
def grabTree(filename):
    import pickle
    fr = open(filename,'rb')
    return pickle.load(fr)

storeTree(myTree,'myTree.txt')#保存到mytree.txt文件中
grabTree('myTree.txt')#加载保存的决策树

{'纹理': {'模糊': '否',
  '清晰': {'根蒂': {'硬挺': '否',
    '稍蜷': {'色泽': {'乌黑': {'触感': {'硬滑': '是', '软粘': '否'}}, '青绿': '是'}},
    '蜷缩': '是'}},
  '稍糊': {'触感': {'硬滑': '否', '软粘': '是'}}}}

2.6、绘制树

上文已经将树创建出来了，下面可以通过这段代码进行决策树的绘制

import matplotlib.pyplot as plt

plt.rcParams['font.sans-serif']=['SimHei']#支持图像显示中文

#boxstyle为文本框的类型，sawtooth是锯齿形，fc是边框线粗细
decisionNode = dict(boxstyle="sawtooth", fc="0.8")
leafNode = dict(boxstyle="round4", fc="0.8")
#定义箭头的属性
arrow_args = dict(arrowstyle="<-")

#绘制节点
def plotNode(nodeTxt, centerPt, parentPt, nodeType):
    createPlot.ax1.annotate(nodeTxt, xy = parentPt, xycoords = 'axes fraction',
                            xytext = centerPt, textcoords = 'axes fraction',
                            va = "center", ha = "center", bbox=nodeType, 
                            arrowprops = arrow_args)

#获取叶节点的数量
def getNumLeafs(myTree):
    #定义叶子节点数目
    numLeafs = 0
    #获取myTree的第一个键
    firstStr = list(myTree.keys())[0]
    #划分第一个键对应的值，即下层树
    secondDict = myTree[firstStr]
    #遍历secondDict
    for key in secondDict.keys():
        #如果secondDict[key]为字典，则递归计算其叶子节点数量
        if type(secondDict[key]).__name__ == 'dict':
            numLeafs += getNumLeafs(secondDict[key])
        else:
            #是叶子节点累计
            numLeafs +=1
    return numLeafs

#获取树的层数
def getTreeDepth(myTree):
    #定义树的层数
    maxDepth = 0
    firstStr = list(myTree.keys())[0]
    secondDict = myTree[firstStr]
    for key in secondDict.keys():
        #如果secondDict[key]为字典，则递归计算其层数
        if type(secondDict[key]).__name__ == 'dict':
            thisDepth = 1 + getTreeDepth(secondDict[key])
        else:
            thisDepth = 1
        #当前层数大于最大层数
        if thisDepth > maxDepth:
            maxDepth = thisDepth
    return maxDepth

#绘制节点文本
def plotMidText(cntrPt, parentPt, txtString):
    #求中间点横坐标
    xMid = (parentPt[0] - cntrPt[0])/2.0 + cntrPt[0]
    #求中间点纵坐标
    yMid = (parentPt[1] - cntrPt[1])/2.0 + cntrPt[1]
    #绘制结点
    createPlot.ax1.text(xMid, yMid, txtString)

#绘制决策树
def plotTree(myTree, parentPt, nodeTxt):
    numLeafs = getNumLeafs(myTree)#叶子节点数
#    depth = getTreeDepth(myTree)#层数
    firstStr = list(myTree.keys())[0]#第一层键
    #计算坐标，
    cntrPt=(plotTree.xOff + (1.0+float(numLeafs))/2.0/plotTree.totalW, plotTree.yOff)
    #绘制中间节点
    plotMidText(cntrPt, parentPt, nodeTxt)
    #绘制决策树节点
    plotNode(firstStr,cntrPt, parentPt, decisionNode)
    secondDict = myTree[firstStr]
    plotTree.yOff = plotTree.yOff-1.0/plotTree.totalD
    for key in secondDict.keys():
        if type(secondDict[key]).__name__ == 'dict':
            #递归绘制决策树
            plotTree(secondDict[key], cntrPt, str(key))
        else:
            #叶子节点横坐标
            plotTree.xOff = plotTree.xOff+1.0/plotTree.totalW
            #绘制叶子节点
            plotNode(secondDict[key], (plotTree.xOff,plotTree.yOff), cntrPt,leafNode)
            plotMidText((plotTree.xOff,plotTree.yOff), cntrPt, str(key))
    #纵坐标
    plotTree.yOff = plotTree.yOff+1.0/plotTree.totalD

def createPlot(inTree):
    #定义图像界面
    fig = plt.figure(1, facecolor='white', figsize = (10,8))
    #初始化
    fig.clf()
    #定义横纵坐标轴
    axprops = dict(xticks = [],yticks = [])
    #初始化图像
    createPlot.ax1 = plt.subplot(111, frameon = False,**axprops)
    #宽度
    plotTree.totalW = float(getNumLeafs(inTree))
    #高度
    plotTree.totalD = float(getTreeDepth(inTree))
    #起始横坐标
    plotTree.xOff = -0.5/plotTree.totalW
    #起始纵坐标
    plotTree.yOff = 1.0
    #绘制决策树
    plotTree(inTree,(0.5,1.0), '')
    #显示图像
    plt.show()

createPlot(myTree)

2.7、使用Scikit - Learn库实现决策树

Scikit-Learn库是Python一个第三方的机器学习模块，它基于NumPy，Scipy，Matplotlib的基础构建的，是一个高效、简便的数据挖掘、数据分析的模块。在后续的学习过程中，我也通过其进行机器学习的实例实现。
下面是基于信息熵简单得到该决策树的代码实现。

import numpy as np
import pandas as pd
from sklearn import tree

'''由于在此库中需要使用数值进行运算，这里需要对样本集进行处理'''
data = pd.read_csv('data1.txt', '\t', index_col='Idx')
labels = np.array(data['label'])
dataSet = np.array(data[data.columns[:-1]])

clf = tree.DecisionTreeClassifier(criterion = 'entropy')#参数criterion = 'entropy'为基于信息熵，‘gini’为基于基尼指数
clf.fit(dataSet, labels)#训练模型

with open("tree.dot", 'w') as f:#将构建好的决策树保存到tree.dot文件中
    f = tree.export_graphviz(clf,feature_names = np.array(data.columns[:-1]), out_file = f)

这里我们需要通过Graphviz将保存好的tree.dot文件绘制出来，在这之前，需要安装Graphviz这个软件。
安装步骤如下：

• 打开http://www.graphviz.org/Download_windows.php ，下载此文件；
  

  

• 打开下载好的文件graphviz-2.38，一直next安装完成；

  
  

• 打开系统属性，编辑环境变量，添加graphviz-2.38的安装目录下的\bin文件夹路径到新变量中，确定即可；

  
  
  

• 打开命令提示符，输入：dot -version查看环境变量是否设置成功；

  
  

• 命令提示符转到tree.dot文件所在位置，键入以下命令：dot tree.dot -Tpng -o tree.png，将决策树文件转化为图像文件。

  
  

  经过上述过程，我们得到了决策树图像。

  
  

上述代码只是基于Scikit-Learn库简单实现决策树，不能体现这个机器学习库的强大之处，后续会介绍如何使用这个库训练模型、测试模型等。

2.8、不足及改进

本文研究了基于信息增益、信息增益率和基尼指数三种划分准则进行决策树的构造，通过“西瓜”样本集实现了其决策树的构造。但是决策树的构造过程中还存在过拟合，即生成的树需要剪枝的情况，以及对于连续变量的处理问题，在下一篇文章中，将针对这两个问题改进相应的代码，从而使构建出的决策树更为严谨准确。

3、参考资料

[1] 周志华. 机器学习.清华大学出版社，2016
[2] Peter Harrington. 机器学习实战. 人民邮电出版社，2013
[3] http://m.blog.csdn.net/article/details?id=51057311
[4] http://www.tuicool.com/articles/uUry2uq