美文网首页
AC自动机+矩阵乘法

AC自动机+矩阵乘法

作者: Gitfan | 来源:发表于2017-03-06 00:41 被阅读0次

DNA Sequence
题意：
有m种DNA序列是有疾病的，问有多少种长度为n的DNA序列不包含任何一种有疾病的DNA序列。（仅含A,T,C,G四个字符）
题解1: 　　题解2:　　题解3:　　　参考1

以下内容参考自这里
样例m=4,n=3,{“AA”,”AT”,”AC”,”AG”}
答案为36，表示有36种长度为3的序列可以不包含疾病
这个和矩阵有什么关系呢？？？


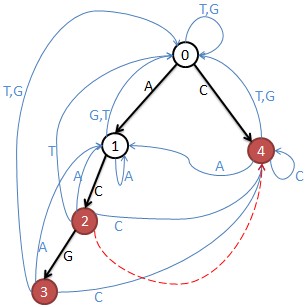
•上图是例子{“ACG”,”C”},构建trie图后如图所示，从每个结点出发都有4条边（A,T,C,G）
•从状态0出发走一步有4种走法：
–走A到状态1（安全）；
–走C到状态4（危险）；
–走T到状态0（安全）；
–走G到状态0（安全）；
•所以当n=1时，答案就是3
•当n=2时，就是从状态0出发走2步，就形成一个长度为2的字符串，只要路径上没有经过危险结点，有几种走法，那么答案就是几种。依此类推走n步就形成长度为n的字符串。
•建立trie图的邻接矩阵M：
2 1 0 0 1
2 1 1 0 0
1 1 0 1 1
2 1 0 0 1
2 1 0 0 1
M[i,j]表示从结点i到j只走一步有几种走法。
那么M的n次幂就表示从结点i到j走n步有几种走法。

题解:
就是通过AC自动机得到合法的转移,然后对应的方法数+1

这是通过构建trie图的代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
#include<map>
#include<string>
using namespace std;
const int MAXN=110;
const long long MOD=100000l;
struct Node
{
    bool virus;
    int fail;
    int next[4];
};
Node trie[MAXN];
int trie_s;
int key(char c)
{
    int index=4;
    switch(c)
    {
        case 'A':index--;
        case 'C':index--;
        case 'G':index--;
        case 'T':index--;
    }
    return index;
}
long long A[MAXN][MAXN],R[MAXN][MAXN];
void insert(char *str)
{
    int len=strlen(str);
    int p=1;
    for(int i=0;i<len;i++)
    {
        int pos=key(str[i]);
        if(!trie[p].next[pos])
        {
            trie[p].next[pos]=++trie_s;
        }
        p=trie[p].next[pos];
    }
    trie[p].virus=true;
}
void getFail()
{
    queue<int> que;
    que.push(1);
    int curr,son,temp;
    while(!que.empty())
    {
        curr=que.front();
        que.pop();
        for(int i=0;i<4;i++)
        {
            son=trie[curr].next[i];
            if(son==0)
            {
                if(curr==1) trie[curr].next[i]=1;
                else trie[curr].next[i]=trie[trie[curr].fail].next[i];
            }
            else
            {
                if(curr==1) trie[son].fail=1;
                else
                {
                    temp=trie[curr].fail;
                    while(temp!=0)
                    {
                        if(trie[temp].next[i])
                        {
                            trie[son].fail=trie[temp].next[i];
                            break;
                        }
                        temp=trie[temp].fail;
                    }
                    if(temp==0) trie[son].fail=1;
                    if(temp!=0&&trie[trie[son].fail].virus) trie[son].virus=true;
                }
                que.push(son);
            }
        }
    }
}
void getPreMatrix()
{
    int son;
    memset(A,0,sizeof(A));
    for(int i=1;i<=trie_s;i++)
    {
        if(trie[i].virus) continue;
        for(int j=0;j<4;j++)
        {
            son=trie[i].next[j];
            if(trie[son].virus) continue;
            A[i][son]++;
        }
    }
}
void matrixMulti(long long a[MAXN][MAXN],long long b[MAXN][MAXN])
{
    long long c[MAXN][MAXN];
    memset(c,0,sizeof(c));
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            for(int k=1;k<=trie_s;k++)
            {
                c[i][j]=(c[i][j]+a[i][k]*b[k][j])%MOD;
            }
        }
    }
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            a[i][j]=c[i][j];
        }
    }
}
void getResMatrix(int n)
{
    memset(R,0,sizeof(R));
    for(int i=1;i<=trie_s;i++)
    {
        R[i][i]=1;
    }
    while(n)
    {
        if(n&1) matrixMulti(R,A);
        matrixMulti(A,A);
        n>>=1;
    }
}
int main()
{

    long long res;
    int m,n;
    scanf("%d%d",&m,&n);
    trie_s=1;
    char str[16];
    while(m--)
    {
        scanf("%s",str);
        insert(str);
    }
    getFail();
    getPreMatrix();
    getResMatrix(n);
    res=0;
    for(int i=1;i<=trie_s;i++)
    {
        res=(res+R[1][i])%MOD;
    }
    printf("%lld\n",res);
    return 0;
}

以下是在转移时强行判断是否可以转移的代码

数组多叉树

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int MAXN=110;
long long A[MAXN][MAXN],R[MAXN][MAXN];
const long long MOD=100000l;
struct Node
{
    int fail;
    int next[4];
    bool virus;
};
int index(char c)
{
    switch(c)
    {
        case 'A':return 0;
        case 'C':return 1;
        case 'G':return 2;
        case 'T':return 3;
    }
}
Node trie[MAXN];
int trie_s;
void insert(char *str)
{
    int len=strlen(str);
    int p=1;
    for(int i=0;i<len;i++)
    {
        int pos=index(str[i]);
        if(!trie[p].next[pos]) trie[p].next[pos]=++trie_s;
        p=trie[p].next[pos];
    }
    trie[p].virus=true;
}
void getFail()
{
    int p=1,son,temp,curr;
    queue<int> que;
    que.push(p);
    while(!que.empty())
    {
        curr=que.front();
        que.pop();
        for(int i=0;i<4;i++)
        {
            son=trie[curr].next[i];
            if(son)
            {
                if(curr==1) trie[son].fail=1;
                else
                {
                    temp=trie[curr].fail;
                    while(temp)
                    {
                        if(trie[temp].next[i])
                        {
                            trie[son].fail=trie[temp].next[i];
                            break;
                        }
                        temp=trie[temp].fail;
                    }
                    if(temp==0) trie[son].fail=1;
                    if(temp&&trie[trie[son].fail].virus) trie[son].virus=true;
                    //如果转移的地方是病毒,那么原来的位置也是病毒;比如BC是病毒,有一个序列为ABCDEF,那么ABCDEF中C的转移指向BC中的C,但BC是病毒结尾,那么ABCDEF也是病毒
                }
                que.push(son);
            }
        }
    }
}
void getPreMatrix()
{
    int son,temp;
    for(int i=1;i<=trie_s;i++)
    {
        if(trie[i].virus) continue;
        for(int j=0;j<4;j++)
        {
            son=trie[i].next[j];
            if(son&&!trie[son].virus) A[i][son]++;
            else if(!son)
            {
                if(i==1) A[1][1]++;
                else
                {
                    temp=i;
                    while(!trie[temp].next[j]&&temp!=1) temp=trie[temp].fail;
                    if(trie[temp].next[j]&&!trie[trie[temp].next[j]].virus) A[i][trie[temp].next[j]]++;
                    else if(!trie[temp].next[j]&&temp==1) A[i][1]++;
                }
            }
        }
    }
}
void matrixMulti(long long a[MAXN][MAXN],long long b[MAXN][MAXN])
{
    long long c[MAXN][MAXN];
    memset(c,0,sizeof(c));
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            for(int k=1;k<=trie_s;k++)
            {
                c[i][j]=(c[i][j]+a[i][k]*b[k][j])%MOD;
            }
        }
    }
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            a[i][j]=c[i][j];
        }
    }
}
void getResMatrix(int n)
{
    memset(R,0,sizeof(R));
    for(int i=1;i<=trie_s;i++)
    {
        R[i][i]=1;
    }
    while(n)
    {
        if(n&1) matrixMulti(R,A);
        matrixMulti(A,A);
        n>>=1;
    }
}
int main()
{

    long long res;
    int m,n;
    scanf("%d%d",&m,&n);
    trie_s=1;
    char str[16];
    while(m--)
    {
        scanf("%s",str);
        insert(str);
    }
    getFail();
    getPreMatrix();
    getResMatrix(n);
    res=0;
    for(int i=1;i<=trie_s;i++)
    {
        res=(res+R[1][i])%MOD;
    }
    printf("%lld\n",res);
    return 0;
}

指针多叉树

#include<cstdio>
#include<cstring>
#include<queue>
using namespace std;
const int MAXN=110;
long long A[MAXN][MAXN],R[MAXN][MAXN];
const long long MOD=100000l;
struct Node
{
    int num;
    Node *fail;
    Node *next[4];
    bool virus;
    void init()
    {
        fail=NULL;
        memset(next,NULL,sizeof(next));
        virus=false;
    }
};
Node *root;
int trie_s;
int index(char c)
{
    switch(c)
    {
        case 'A':return 0;
        case 'C':return 1;
        case 'G':return 2;
        case 'T':return 3;
    }
}
void insert(char *str)
{
    int len=strlen(str);
    Node *p=root;
    for(int i=0;i<len;i++)
    {
        int pos=index(str[i]);
        if(p->next[pos]==NULL)
        {
            p->next[pos]=new Node();
            p->next[pos]->init();
            p->next[pos]->num=++trie_s;
        }
        p=p->next[pos];
    }
    p->virus=true;
}
void getFail()
{
    Node *p=root,*son,*temp;
    queue<Node *>que;
    que.push(p);
    while(!que.empty())
    {
        Node *curr=que.front();
        que.pop();
        for(int i=0;i<4;i++)
        {
            son=curr->next[i];
            if(son!=NULL)
            {
                if(curr==root) son->fail=root;
                else
                {
                    temp=curr->fail;
                    while(temp!=NULL)
                    {
                        if(temp->next[i]!=NULL)
                        {
                            son->fail=temp->next[i];
                            break;
                        }
                        temp=temp->fail;
                    }
                    if(temp==NULL) son->fail=root;
                    if(temp!=NULL&&son->fail->virus) son->virus=true;
                }
                que.push(son);
            }
        }
    }
}
void getPreMatrix()
{
    Node *p=root,*son,*temp;
    queue<Node *>que;
    que.push(p);
    while(!que.empty())
    {
        Node *curr=que.front();
        que.pop();
        if(curr->virus) continue;
        for(int i=0;i<4;i++)
        {
            son=curr->next[i];
            if(son!=NULL&&!son->virus)
            {
                A[curr->num][son->num]++;
            }
            else if(son==NULL)
            {
                if(curr==root) A[1][1]++;
                else
                {
                    temp=curr;
                    while(temp->next[i]==NULL&&temp!=root) temp=temp->fail;
                    if(temp->next[i]&&!temp->next[i]->virus) A[curr->num][temp->next[i]->num]++;
                    else if(temp->next[i]==NULL&&temp==root) A[curr->num][1]++;
                }
            }
            if(son!=NULL) que.push(son);
        }
    }
}
void matrixMulti(long long a[MAXN][MAXN],long long b[MAXN][MAXN])
{
    long long c[MAXN][MAXN];
    memset(c,0,sizeof(c));
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            for(int k=1;k<=trie_s;k++)
            {
                c[i][j]=(c[i][j]+a[i][k]*b[k][j])%MOD;
            }
        }
    }
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            a[i][j]=c[i][j];
        }
    }
}
void getResMatrix(int n)
{
    memset(R,0,sizeof(R));
    for(int i=1;i<=trie_s;i++)
    {
        R[i][i]=1;
    }
    while(n)
    {
        if(n&1) matrixMulti(R,A);
        matrixMulti(A,A);
        n>>=1;
    }
}
int main()
{
    long long res;
    int m,n;
    scanf("%d%d",&m,&n);
    root=new Node();
    root->init();
    root->num=1;
    trie_s=1;
    char str[16];
    while(m--)
    {
        scanf("%s",str);
        insert(str);
    }
    getFail();
    getPreMatrix();
    getResMatrix(n);
    res=0;
    for(int i=1;i<=trie_s;i++)
    {
        res=(res+R[1][i])%MOD;
    }
    printf("%lld\n",res);
    return 0;
}

考研路茫茫——单词情结
题意:
给出n个单词词根,求出长度为1-L的所有由小写字母组成的并且至少包含一个单词词根的数目
题解:
　　因为题目要求的是至少包含一个词根的单词数目,所以我们容易想到它的反面,即一个词根也不包含单词数目;
　　设长度为len的单词中,一个词根也不包含的单词数目为sum,容易知道,sum的求法和上面的DNS序列那道题类似,即sum=Alen;而长度为len的总的单词数目为26len;
　　所以结果为26len-Alen;则最后的结果为26+262+......+26len-(A+A2+...+Alen);这里涉及到等比矩阵求和

#include<cstdio>
#include<cstring>
#include<queue>
#include<cmath>
#include<iostream>
typedef unsigned long long ULL;
using namespace std;
const int MAXN=35;
int trie_s;
struct Matrix
{
    ULL arr[MAXN][MAXN];
    void init()
    {
        memset(arr,0,sizeof(arr));
        for(int i=1;i<=trie_s;i++)
        {
            arr[i][i]=1;
        }
    }
}A,R;
Matrix add(Matrix a,Matrix b)
{
    Matrix c;
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            c.arr[i][j]=a.arr[i][j]+b.arr[i][j];
        }
    }
    return c;
}
Matrix multi(Matrix a,Matrix b)
{
    Matrix c;
    memset(c.arr,0,sizeof(c));
    for(int i=1;i<=trie_s;i++)
    {
        for(int j=1;j<=trie_s;j++)
        {
            for(int k=1;k<=trie_s;k++)
            {
                c.arr[i][j]+=a.arr[i][k]*b.arr[k][j];
            }
        }
    }
    return c;
}
Matrix pow(Matrix a,int b)
{
    Matrix res;
    res.init();
    while(b)
    {
        if(b&1) res=multi(res,a);
        a=multi(a,a);
        b>>=1;
    }
    return res;
}
Matrix sum(Matrix a,int n)
{
    if(n==1) return a;
    Matrix tmp;
    tmp.init();
    tmp=add(tmp,pow(a,n>>1));
    tmp=multi(tmp,sum(a,n>>1));
    if(n&1) tmp=add(tmp,pow(a,n));
    return tmp;
}
struct Node
{
    int fail;
    int next[26];
    bool ed;
    void init()
    {
        fail=0;
        ed=false;
        memset(next,0,sizeof(next));
    }
};
Node trie[MAXN];
void insert(char *str)
{
    int len=strlen(str);
    int p=1;
    for(int i=0;i<len;i++)
    {
        int pos=str[i]-'a';
        if(!trie[p].next[pos])
        {
            trie[p].next[pos]=++trie_s;
            trie[trie[p].next[pos]].init();
        }
        p=trie[p].next[pos];
    }
    trie[p].ed=true;
}
void getFail()
{
    queue<int> que;
    int p=1,son,temp;
    que.push(p);
    while(!que.empty())
    {
        int curr=que.front();
        que.pop();
        for(int i=0;i<26;i++)
        {
            son=trie[curr].next[i];
            if(son)
            {
                if(curr==1) trie[son].fail=1;
                else
                {
                    temp=trie[curr].fail;
                    while(temp!=0)
                    {
                        if(trie[temp].next[i])
                        {
                            trie[son].fail=trie[temp].next[i];
                            break;
                        }
                        temp=trie[temp].fail;
                    }
                    if(!temp) trie[son].fail=1;
                    if(temp&&trie[trie[son].fail].ed) trie[son].ed=true;
                }
                que.push(son);
            }
        }
    }
}
void getPreMatrix()
{
    memset(A.arr,0,sizeof(A.arr));
    int temp,son;
    for(int i=1;i<=trie_s;i++)
    {
        if(trie[i].ed) continue;
        for(int j=0;j<26;j++)
        {
            son=trie[i].next[j];
            if(son&&!trie[son].ed) A.arr[i][son]++;
            else if(!son)
            {
                if(i==1) A.arr[1][1]++;
                else
                {
                    temp=i;
                    while(!trie[temp].next[j]&&temp!=1) temp=trie[temp].fail;
                    if(trie[temp].next[j]&&!trie[trie[temp].next[j]].ed) A.arr[i][trie[temp].next[j]]++;
                    else if(!trie[temp].next[j]&&temp==1)
                    {
                        A.arr[i][1]++;
                    }
                }
            }
        }
    }
}
ULL pow(ULL a,int n)
{
    ULL res=1;
    while(n)
    {
        if(n&1) res=res*a;
        a=a*a;
        n>>=1;
    }
    return res;
}
ULL powSum(ULL a,int n)
{
    if(n==1) return a;
    ULL res=(1+pow(a,n>>1))*powSum(a,n>>1);
    if(n&1) res=res+pow(a,n);
    return res;
}
int main()
{
    int n,l;
    char str[10];
    while(scanf("%d%d",&n,&l)!=EOF)
    {
        trie_s=1;
        trie[1].init();
        for(int i=0;i<n;i++)
        {
            scanf("%s",str);
            insert(str);
        }
        getFail();
        getPreMatrix();
        A=sum(A,l);
        ULL total=powSum(26,l);
        ULL res=0;
        for(int i=1;i<=trie_s;i++)
        {
            res+=A.arr[1][i];
        }
        cout<<total-res<<endl;
    }
    return 0;
}

相关文章

  • AC自动机+矩阵乘法

    DNA Sequence题意：有m种DNA序列是有疾病的，问有多少种长度为n的DNA序列不包含任何一种有疾病的DN...

  • AC自动机 专题整理

    AC自动机学习记录 参考资料 字典树（讲解+模版）AC自动机算法AC自动机算法详解hdu 2222 ac自动机入门...

  • 自动AC机？不，是AC自动机

    今天我们来介绍一点进阶的知识——AC自动机。 AC自动机是啥 AC自动机是什么呢？是不是用了这个算法，不管什么题目...

  • 【AC自动机】AC自动机可以帮你自动AC吗

    参考博文：AC自动机算法详解 （转载） （原文作者：DarkRaven，原文的链接失效了）图片来源：AC自动机算...

  • AC自动机-去除敏感字符

    AC自动机 AC自动机：Aho-Corasick automation，该算法在1975年产生于贝尔实验室，是著名...

  • lucene中文分词

    IK中文分词 DoubleArrayTrie的AC自动机

  • 字符串算法小结

    hash kmp和ac自动机 后缀数组，后缀自动机，后缀树 扩展kmp manacher算法 回文自动机 可删改的...

  • 图形变换原理

    概述: 图形变换大体分为缩放,平移,拉伸,旋转.他们的原理是矩阵的乘法. 矩阵的乘法: 矩阵的乘法规则:两个矩阵相...

  • 矩阵乘法在python中的表示

    从数学表达上来说，矩阵乘法有： 矩阵的乘法(matmul product)：这就是线性代数里面的矩阵乘法 內积/点...

  • sparse matrix 的分布式存储和计算

    矩阵乘法 我们先来补充一下矩阵乘法的数学知识： 矩阵乘法的意义: 对一个矩阵进行左乘一个矩阵的运算，相当于对该矩阵...

网友评论

      本文标题：AC自动机+矩阵乘法

      本文链接：https://www.haomeiwen.com/subject/ixlygttx.html

      延伸阅读

      深度阅读

      • 您也可以注册成为美文阅读网的作者，发表您的原创作品、分享您的心情！

      栏目导航

      热点阅读

      关于我们|服务条款|联系我们|AC自动机+矩阵乘法|投稿指南|网站地图|RSS订阅|排版工具|手机版

      提供经典美文摘抄,优美散文欣赏,现代诗歌精选,短篇小说,心情随笔,表白情书范文,故事会在线阅读欣赏

      Copyright © 2014-2023 Haomeiwen.com All Rights Reserved. 好美文阅读网 版权所有

      备案信息：桂公网安备 45052102000051号 · 桂ICP备13007215号-3

      本站所收录作品、热点评论等信息部分来源互联网，目的只是为了系统归纳学习和传递资讯

      所有作品版权归原创作者所有，与本站立场无关，如不慎侵犯了你的权益，请联系我们告知，我们将做删除处理！