从泊松分布开始聊 CCD 参数

日常生活中，大量事件用平均值描述，如某医院平均每小时出生3个婴儿，某公司平均每 10 分钟接到 1 个电话。但平均值只表示事件的总数，没法知道事件发生的具体时间。

泊松分布 可以描述某段时间内，事件发生的概率。

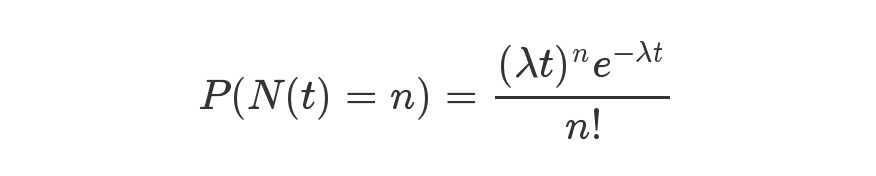泊松分布公式

上图为泊松分布的公式。等号的左边，P 表示概率，N 表示某种函数关系，t 表示时间，n 表示数量，1 小时内出生 3 个婴儿的概率，就表示为 P( N(1) = 3 ) 。

同样，测量电流强度、光强度时，能够给出收集到的电子或光子的平均数量，但无法得知任意时刻实际收集到的电子或光子数量。每一时刻的实际电子/光子数量可能会高于、低于或相当于平均的数量，其分布按平均值遵循泊松分布。这种实验观测中的读出噪声，称为散粒噪声。

泊松分布在大量粒子数时趋向于正态分布，同时其期望与方差相等。

在固定背景，大量粒子时，信噪比为（N 为粒子数，标准差即为噪声）：

信噪比

所以，当测量值大于 N + 3sqrt（N） 时，认为有 99.730020% 的概率，称为最小检出线，测量值可信。

在信噪比固定时，相机能记录的最亮与最暗的入射亮度之比称为动态范围。讨论动态范围时，一定要固定背景/信噪比。如上述例子，若背景为 N，则最暗亮度为 N + 3sqrt（N），最大亮度若为 Nmax，则动态范围为 Nmax / N + 3sqrt（N）。

CCD 中除了散粒噪声，还包括电路噪声，例如放大器的读出噪声等。在粒子数较少时，散粒噪声占主导地位，而在粒子数较多时，电路噪声占主导地位。

阱深表示每个相元可以储存的电荷数，阱深越大，理论上能存储的电子也越多，能够达到的信噪比也越高。

暗电流指没有光的状态下 CCD 产生的电流，与温度密切相关。温度越低，暗电流越小。

参考文献：

1.https://zh.wikipedia.org/wiki/%E6%95%A3%E7%B2%92%E5%99%AA%E5%A3%B0

2.https://zh.wikipedia.org/wiki/%E6%AD%A3%E6%80%81%E5%88%86%E5%B8%83

3.https://zh.wikipedia.org/wiki/%E6%B3%8A%E6%9D%BE%E5%88%86%E4%BD%88

4.http://www.ruanyifeng.com/blog/2015/06/poisson-distribution.html