从多项式相加看线性结构

给出两个多项式： 大家都很清楚多项式相加，即为相同指数项对应相加。那我们如何使用程序来描述两个多项式相加呢？大家首先想到的是用数组描述，多项式的指数使用下标来表示，前面的系数为对应数组中的值。f1(x)表示如下： f2(x)表示如下： 其实只要写个for循环，相同下标的相加即可，非常简单。下面问题来了，如果面对的多项式是类似 这种形式的话，0项太多，上面的这种办法就会很冗余，白白浪费空间。因此需要采取另外的办法来描述。上面的方式问题出在我们使用数组下标用来描述指数，当指数很大的时，就会出现很多系数为0项，我们的想法是不要0项，只将非0项存储起来进行描述。因此我们可以将系数和指数绑定到一起作为一个整体，类似这种方式(系数，指数)。还是上面两个多项式，采用结构体+数组的方式进行描述。f1(x)表示如下： f2(x)表示如下： 其中指数是按照由大到小的顺序存储。大家可以看到指数很大的时候，也不会浪费存储空间。下面我们用C程序来实现。

#include<stdio.h>
#define F1_LENGTH 3
#define F2_LENGTH 3
struct Node
{
    int coef;
    int expon;

};
struct Node f1_nodes[3];
struct Node f2_nodes[3];
void main(){
    f1_nodes[0].coef = 3;
    f1_nodes[0].expon = 4;

    f1_nodes[1].coef = 4;
    f1_nodes[1].expon = 2;

    f1_nodes[2].coef = 1;
    f1_nodes[2].expon = 0;

    f2_nodes[0].coef = 5;
    f2_nodes[0].expon = 3;

    f2_nodes[1].coef = 4;
    f2_nodes[1].expon = 2;

    f2_nodes[2].coef = 8;
    f2_nodes[2].expon = 0;
    size_t i = 0, j = 0;
    for (; i < F1_LENGTH && j < F2_LENGTH;)
    {
        if (f1_nodes[i].expon > f2_nodes[j].expon){

            printf("(%d,%d) ", f1_nodes[i].coef, f1_nodes[i].expon);
            i++;
        
        }else if (f1_nodes[i].expon < f2_nodes[j].expon){
            printf("(%d,%d) ", f2_nodes[j].coef, f2_nodes[j].expon);
            j++;
        }else
        {
            printf("(%d,%d) ", f1_nodes[i].coef+f2_nodes[j].coef, f2_nodes[j].expon);
            i++;
            j++;
        }
    }
    while (i<F1_LENGTH)
    {
        printf("(%d,%d) ", f1_nodes[i].coef, f1_nodes[i].expon);
        i++;
    }
    while (j<F2_LENGTH)
    {
        printf("(%d,%d) ", f2_nodes[j].coef, f2_nodes[j].expon);
        j++;
    }
    getchar();
}

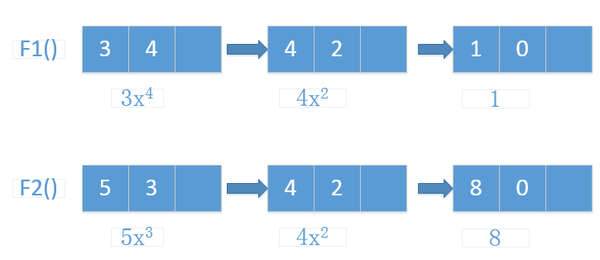
通过上面的方式即可完成多项式的计算，但是上面的方式依然不是特别好，因为数组的大小是固定的，没办法动态改变，接下来我们使用链表的方式来存储非零项，定义如下数据类型:

typedef struct Node *PolyLink;
struct Node
{
int coef;
int expon;
PolyLink link;

};

f1和f2链表存储形式为：

C语言实现如下：

#include<stdio.h>
#include <malloc.h>
typedef struct Node *PolyLink;
struct Node
{
    int coef;
    int expon;
    PolyLink link;
};
void main(){
    PolyLink p,p1;
    PolyLink head1 = (PolyLink)malloc(sizeof(struct Node));
    p = head1;
    p->coef = 3;
    p->expon = 4;
    p->link = (PolyLink)malloc(sizeof(struct Node));

    p = p->link;
    p->coef = 4;
    p->expon = 2;
    p->link = (PolyLink)malloc(sizeof(struct Node));

    p = p->link;
    p->coef = 1;
    p->expon = 0;
    p->link = NULL;

    PolyLink head2 = (PolyLink)malloc(sizeof(struct Node));
    p = head2;
    p->coef = 5;
    p->expon = 3;
    p->link = (PolyLink)malloc(sizeof(struct Node));

    p = p->link;
    p->coef = 4;
    p->expon = 2;
    p->link = (PolyLink)malloc(sizeof(struct Node));

    p = p->link;
    p->coef = 8;
    p->expon = 0;
    p->link = NULL;

    while(head1 != NULL && head2 != NULL){

        if (head1->expon > head2->expon){
            printf("(%d,%d) ", head1->coef, head1->expon);
            p1 = head1;
            head1 = head1->link;
            free(p1);
        }
        else if (head1->expon < head2->expon){

            printf("(%d,%d) ", head2->coef, head2->expon);
            p1 = head2;
            head2 = head2->link;
            free(p1);
        
        }
        else{
            printf("(%d,%d) ", head1->coef+head2->coef, head2->expon);
            p1 = head1;
            head1 = head1->link;
            free(p1);
            p1 = head2;
            head2 = head2->link;
            free(p1);
        
        }
    
    }
    while (head1 != NULL){
        printf("(%d,%d) ", head1->coef, head1->expon);
        p1 = head1;
        head1 = head1->link;
        free(p1);
    }
    while (head2 != NULL){
        printf("(%d,%d) ", head2->coef, head2->expon);
        p1 = head2;
        head2 = head2->link;
        free(p1);

    }
    getchar();

}